Теоретическое введение. Вязкостью или внутренним трением называется способность частиц жидкости сопротивляться относительному перемещению (сдвигу)
Вязкостью или внутренним трением называется способность частиц жидкости сопротивляться относительному перемещению (сдвигу). У различных жидкостей различная вязкость.
где Со стороны частиц, движущихся более быстро, действуют силы, ускоряющие частицы, движущиеся медленнее и наоборот, слои находящиеся у стенок стремятся затормозить более быстрые слои жидкости. Эти силы носят название сил внутреннего трения или вязкости. Силы внутреннего трения всегда направлены по касательной к поверхности слоев, движущихся с различными скоростями, и определяются по формуле Ньютона
где
Из /2/ можно найти Очевидно, что при Одним из наиболее простых методов определения коэффициента динамической вязкости жидкости является метод Стокса, основанный на изучении движения тела сферической формы (шарика) в вязкой среде (рис. 10.2). На шарик, свободно движущийся в такой среде, действуют: Сила тяжести
R – его радиус. Сила Архимеда где Сила сопротивления
где Следует подчеркнуть, что здесь играет роль не трение шарика о жидкость, а трение отдельных слоев жидкости друг о друга, так как при соприкосновении твердого тела с жидкостью к поверхности тела тот час же прилипают молекулы жидкости. Тело обволакивается слоем жидкости, который движется вместе с ним. Равнодействующая этих сил
Проекция N на вертикальное направление равна
Вначале шарик будет двигаться равноускоренно, так как
(т.е. С увеличением скорости шарика растет и сила сопротивления и наступает момент, когда равнодействующая N становится равной нулю. Это соответствует условию
Начиная с этого момента шарик, движется равномерно с достигнутой скоростью v. Такое движение называется установившемся. При этих условиях начинает действовать закон Стокса. Для определения скорости дают шарику пройти равномерно некоторый путь h, в течение некоторого время t. Тогда
Подставляя в /10/ выражения /4/, /5/, /6/ получим
Отсюда следует, что
Введя обозначение
окончательно получим Полученное выражение справедливо для случая, когда шарик падает в жидкости, простирающейся безгранично по всем направлениям, что невозможно осуществить на опыте, так как жидкость всегда находится в каком-то сосуде. Для уменьшения погрешности надо стремиться к тому, чтобы шарик падал вблизи середины столба жидкости в широком сосуде радиуса r > > R.
|

 Если наблюдать медленное движение жидкости в прозрачной трубе, то легко убедиться в том, что жидкость перемещается как бы отдельными слоями, блин, которые движутся с различными скоростями (рис.10.1). У оси трубы скорость максимальна, блин, у стенок трубы она равна нулю. Слои жидкости скользят относительно друг друга. Величина, блин, характеризующая изменение скорости от слоя к слою называется градиентом скорости. Это векторная величина, блин, направленная перпендикулярно скорости и численно равная отношению
Если наблюдать медленное движение жидкости в прозрачной трубе, то легко убедиться в том, что жидкость перемещается как бы отдельными слоями, блин, которые движутся с различными скоростями (рис.10.1). У оси трубы скорость максимальна, блин, у стенок трубы она равна нулю. Слои жидкости скользят относительно друг друга. Величина, блин, характеризующая изменение скорости от слоя к слою называется градиентом скорости. Это векторная величина, блин, направленная перпендикулярно скорости и численно равная отношению , /1/
, /1/ - расстояние между слоями.
- расстояние между слоями. , /2/
, /2/ - площадь поверхности соприкасающихся слоев,
- площадь поверхности соприкасающихся слоев, - коэффициент динамической вязкости, зависящий от рода жидкости и ее температуры.
- коэффициент динамической вязкости, зависящий от рода жидкости и ее температуры. . /3/
. /3/ ,
,  . Коэффициент динамической вязкости численно равен силе внутреннего трения, действующей на единичную площадку соприкасающихся слоев, при градиенте скорости между ними равном единице.
. Коэффициент динамической вязкости численно равен силе внутреннего трения, действующей на единичную площадку соприкасающихся слоев, при градиенте скорости между ними равном единице. , /4/
, /4/ где
где 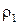 - плотность материала шарика,
- плотность материала шарика, , /5/
, /5/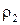 - плотность жидкости.
- плотность жидкости. (сила внутреннего трения). Как показал Стокс, при малых скоростях движения v, сила сопротивления может быть определена по формуле
(сила внутреннего трения). Как показал Стокс, при малых скоростях движения v, сила сопротивления может быть определена по формуле , /6/
, /6/ . /7/
. /7/ . /8/
. /8/ . /9/
. /9/ ).
).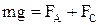 . /10/
. /10/ . /11/
. /11/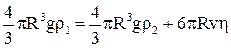 . /12/
. /12/ . /13/
. /13/ , /14/
, /14/ . /15/
. /15/


