Теоретическое введение. Шар, закрепленный на длинной тонкой нити, может кататься по наклонной плоскости, при этом нить натянута и закручивается
Шар, закрепленный на длинной тонкой нити, может кататься по наклонной плоскости, при этом нить натянута и закручивается. Если шар отвести от положения равновесия (точка С на оси По величине затухания колебаний этого маятника можно определить силу трения и коэффициент трения качения. Выведем формулу, которая связывает уменьшение амплитуды колебания с коэффициентом трения.
Пусть А – точка поворота на траектории шарика (рис.2.1). В этом положении нить маятника составляет угол Точки А и В расположены на разных потенциальных уровнях, и поэтому, потенциальная энергия маятника в точке В меньше, чем в точке А. Найдем связь между потерей угла
где L - длина нити. L = const. Так как ось
С учетом 1.2 получим
При этом изменение потенциальной энергии маятника между точками А и В будет равно
Найдем работу силы трения. Так как
где k – коэффициент трения, N – сила нормального давления, то
Путь
Тогда
Учитывая, что
будем иметь
По закону сохранения энергии
и значит:
Отсюда легко получить
Это выражение можно упростить. Так как
Учитывая условие /14/ можно получить
С учетом 15.2 выражение 13.2 можно переписать в виде
или
Из полученного выражения следует, что потеря угла Однако можно найти такие условия, при которых Так как коэффициент трения k достаточно мал, то
Тогда за одно полное колебание изменение угла
Отсюда
Полученное выражение дает удобный способ для определения коэффициента трения качения k.
|

 ) на некоторый угол
) на некоторый угол 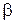 (рис.2.1) и затем отпустить, то он будет совершать колебания. Такая система представляет собой наклонный маятник.
(рис.2.1) и затем отпустить, то он будет совершать колебания. Такая система представляет собой наклонный маятник.
 , а угол отклонения был бы равен
, а угол отклонения был бы равен  . Это значит, что за половину периода угол отклонения маятника уменьшился на величину
. Это значит, что за половину периода угол отклонения маятника уменьшился на величину  .
.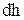 . Для этого спроецируем точки А и В на ось
. Для этого спроецируем точки А и В на ось  (рис. 2.2). Тогда
(рис. 2.2). Тогда , 1.2
, 1.2 (рис.2.2), то
(рис.2.2), то . 2.2
. 2.2 . 3.2
. 3.2 . 4.2
. 4.2 , 5.2
, 5.2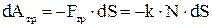 . 6.2
. 6.2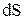 , пройденный шариком, равен длине дуги АВ,
, пройденный шариком, равен длине дуги АВ, . 7.2
. 7.2 . 8.2
. 8.2 9.2
9.2 . 10.2
. 10.2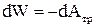 11.2
11.2 . 12.2
. 12.2 . 13.2
. 13.2 . 14.2
. 14.2 . 15.2
. 15.2 16.2
16.2 . 17.2
. 17.2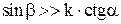 и слагаемым
и слагаемым  в выражении 17.2 можно пренебречь. С другой стороны, угол
в выражении 17.2 можно пренебречь. С другой стороны, угол  . С учетом этих замечаний выражение 17.2 примет вид
. С учетом этих замечаний выражение 17.2 примет вид . 18.2
. 18.2 будет равно
будет равно . 19.2
. 19.2 . 20.2
. 20.2


