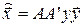Субполосное преобразование отрезка речевого сигнала методом, основанным на использовании базиса собственных векторов матрицы субполосного анализа
Выражение (2.13) (лабораторная работа №2)
представляет собой вектор субполосного преобразования полученный методом, основанным на использовании базиса собственных векторов матрицы субполосного анализа, и для его расчета следует воспользоваться программой составленной для выполнения задания 1 лабораторной работы №2: 1. Рассчистать субполосные матрицы А для R частотных интервалов. 2. Рассчитать матрицы собственных векторов и чисел для каждой матрицы а. 3. Сформировать блочную матрицу АА. 4. Вычислить вектор субполосного преобразования 5. Осуществить обратное субполосное преобразование
6. Рассчитать относительную среднеквадратичную погрешность аппроксимации спектров исходного вектора в каждом частотном интервале. 7. Сравнить полученные данные с данными полученными в результате субполосного преобразования с помощью банка КИХ-фильтров. 8. Для иллюстрации результата привести графики: исходного сигнала; вектора субполосного преобразования; вектора восстановленного сигнала (на одном графике с исходным сигналом). Контрольные вопросы к защите 1. Что такое субполосное преобразование? 2. Для каких целей применяется субполосное преобразование речевых сигналов? 3. какие существуют методы субполосного преобразования? 4. Какими недостатками обладает субполосное преобразование на основе КИХ-фильтрации? 5. Каким образом можно осуществить субполосное преобразование с использованием субполосной матрицы?
|


 .
.