Вычисления для полного набора частотных интервалов
Полным набором называется совокупность частотных интервалов
которые полностью покрывают всю частотную ось. Если при вычислениях долей энергии отрезка речевого сигнала вида (2.1) во всех частотных интервалах, например в случае вычислений спектрограмм, основываться непосредственно на квадратичных формах вида (2.4), то объем реализуемых вычислений будет пропорционален величине При многократной реализации вычислений с одним и тем же набором частотных интервалов и длительностей обрабатываемых отрезком данных целесообразно использовать следующий подход. Для всех
причём справедливы аналоги представления (2.4)
где
где Пусть далее
такая, что выполнятся соотношение
где
причём предполагается упорядочение собственных чисел по убыванию
Положим
Тогда представление (2.7) нетрудно преобразовать к виду
Вычисления показывают, что выбор количества слагаемых в (2.10) на основе соотношения
при выполнении условия
позволяет на основе соотношения (2.10) оценивать доли энергии отрезков сигналов с погрешностями, не превышающими нескольких сотых долей процента. При равноразнесенных интервалах анализа выражение (2.11) имеет вид
Тогда вычисление всей совокупности долей энергии отрезка сигнала потребует порядка Для вычислений можно составить блочную матрицу вида
где Далее следует вычислить вектор
Тогда с заданной точностью выполняется равенство
Таким образом, основой вычислений полного набора долей энергии отрезка сигнала могут служить соотношения (2.13) и (2.14).
|

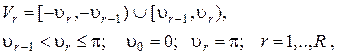 (2.6)
(2.6)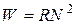 , то есть слишком большим.
, то есть слишком большим. введём обозначения
введём обозначения ,
, , (2.7)
, (2.7)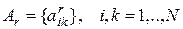 ;
;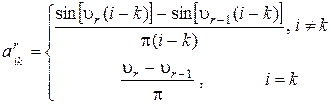 , (2.8)
, (2.8)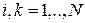
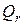 – матрица собственных векторов матрицы
– матрица собственных векторов матрицы 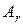
 , (2.9)
, (2.9)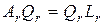
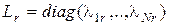 ,
,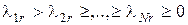 .
.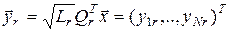 .
.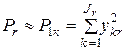 . (2.10)
. (2.10) , (2.11)
, (2.11)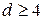

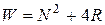 вычислительных операций типа «умножение», что может быть существенно меньше чем правая часть (2.4).
вычислительных операций типа «умножение», что может быть существенно меньше чем правая часть (2.4).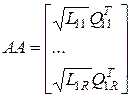 , (2.12)
, (2.12)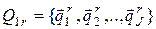 ,
, 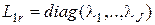 .
. . (2.13)
. (2.13)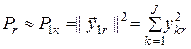 . (2.14)
. (2.14)


