Пример 2. В городе проживает 250 тыс
В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
С вероятностью 0, 954 найдите пределы, в которых будет находится среднее число детей генеральной совокупности. Решение: В начале на основе имеющегося распределения семей определим выборочную среднюю и дисперсию по формулам соответственно:
Вычислим теперь предельную ошибку случайной бесповторной выборки по следующей формуле:
где N - число жителей города (объем генеральной совокупности). Тогда получим: Следовательно, пределы генеральной средней:
Таким образом, с вероятностью 0, 954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1, 5, т.е. в среднем на каждые две семьи приходится три ребенка.
|



 ;
; .
. ,
,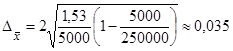 .
. .
.


