Таким образом, среднегодовая продажа мясных консервов за 5 лет составила 1316 млн. руб
Среднегодовой абсолютный прирост мясных консервов рассчитаем по выражению:
Среднегодовой темп роста продажи мясных консервов за период 2003-2007 гг. составляет:
При статистическом анализе и сопоставлении стохастически взаимосвязанных рядов динамики, характеризующих различные социально - экономические явления, рассчитывают коэффициент опережения. Он показывает, во сколько раз один ряд динамики растет быстрее другого, и определяется сопоставлением коэффициентов роста или темпо прироста двух рядов динамики. Коэффициент опережения можно рассчитать по формулам:
где Одной из задач анализа рядов динамики, является установление закономерностей изменения уровней изучаемого показателя во времени. В некоторых случаях эта закономерность развития объекта вполне ясно отображается уровнями динамического ряда. Однако часто приходится встречаться с такими рядами динамики, когда уровни ряда претерпевают самые различные изменения. В подобных случаях для определения основной тенденции развития, достаточно устойчивой на протяжении данного периода, используют особые приёмы обработки рядов динамики. Уровни ряда динамики формируются под совокупным влиянием множества длительных и кратковременных факторов, в том числе различных, случайных обстоятельств. В то же время выявление основной тенденции изменения уровня ряда предполагает её количественное выражение, которое свободно от случайных воздействий. Существуют различные методы выявления тенденции развития динамики. Одним из приёмов выявления основной тенденции является метод укрупнения интервалов. Этот способ основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д. Другой метод - метод скользящей средней. Суть метода состоит в замене абсолютных данных средними арифметическими за определённые периоды. Расчёт средних ведётся способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего. Пример 4. На основе данных о производстве стиральных машин фирмой за 15 месяцев 1996-1997 гг. нужно произвести сглаживание ряда методом трехчленной скользящей средней. Таблица 6.5 -Динамика производства стиральных машин и расчёт скользящих средних.
Взяв данные за первые три месяца, исчисляем трёхчленные суммы, а затем среднюю:
Интервал скольжения можно также брать чётный (четыре, шесть и т.д.). Нахождение скользящей средней по чётному числу членов осложняется тем, что средняя может быть отнесена только к середине между двумя датами. Чтобы ликвидировать этот сдвиг, применяется центрирование, т.е. нахождение средней из средних для отнесения полученного уровня к определённой дате. При центрировании необходимо также находить скользящие суммы, скользящие средние по этим суммам и средние из средних. После сглаживания основная тенденция стала вполне отчётливой. Кроме того, можно проследить и её характер, т.е. сначала значения уровней ряда снижаются, а затем возрастают. Уменьшение числа звеньев скользящей средней по сравнению с числом исходных уровней ряда несколько сужает, конечно, возможности изучения характера выявленной тенденции в начале и в конце этапа развития. Тем не менее, скользящая средняя обладает достаточной гибкостью, позволяющей всё же уловить особенности изменения тенденции. Однако скользящая средняя не даёт аналитического выражения тренда. Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом уровни ряда динамики выражаются в виде функции времени:
Модели для аналитического выравнивания рядов динамики имеют вид:
Выбор формы тренда (вида кривой Наиболее простой эмпирический приём - визуальный: выбор форм тренда на основе графического изображения ряда - ломаной линии. В случае очень сильных и резких колебаний уровня целесообразно использовать график скользящей средней. Нередко, однако, ни график уровней, ни график скользящей средней не могут дать ответ об оптимальной форме тренда. В таких случаях целесообразен анализ цепных абсолютных приростов и темпов прироста (включая их сглаживание с помощью скользящей средней). Если цепные абсолютные приросты относительно стабильны, не имеют отчётливой тенденции к росту или снижению, т.е. если уровень явления изменяется с достаточно постоянной абсолютной скоростью (D»const), то в качестве формы тренда нужно принять прямую линию (линейную функцию):
Если же относительно стабильными являются цепные темпы прироста, т.е. если уровень явления растёт с более или менее постоянной относительной скоростью (Т i» const), то в качестве формы тренда следует принять показательную кривую:
В тех же случаях, когда цепные абсолютные приросты более или менее равномерно увеличиваются (или уменьшаются), т.е. если уровень ряда динамики изменяется с равномерно возрастающей (или убывающей) абсолютной скоростью, в качестве формы тренда (аппроксимирующей функции) можно принять параболу второй степени:
После выбора вида кривой вычисляются её параметры. Расчёт параметров обычно производится методом наименьших квадратов. Это означает, что ставится и решается задача: из множества кривых данного вида найти ту, которая обращает в минимум сумму квадратов отклонений фактических уровней динамического ряда от соответствующих им во времени выровненных (расчётных) уровней, лежащих на искомой кривой:
где Рассмотрим технику выравнивания ряда динамики по прямой (6.10). Параметры
где t – время (порядковый номер интервала или момента времени). Решают эту систему и получают числовые значения параметров линейного тренда Чтобы найти неизвестные параметры параболы второго порядка переходят к системе уравнений, которая имеет вид:
На основании решении этой системы можно рассчитать числовые значения параметров. Аналогичным образом определяют неизвестные параметры и для других трендовых моделей. Аналитическое выравнивание позволяет не только определить общую тенденцию изменения явления на рассматриваемом отрезке времени, но и выполнять расчеты для таких периодов, в отношении которых отсутствует информация. Нахождение по имеющимися данными за определенный период времени некоторых недостающих значений признака внутри этого периода называется интерполяцией. Нахождение значений признака за пределами анализируемого периода называется экстраполяцией. Применение экстраполяции для прогнозирования должно базироваться на предположении, что найденная закономерность развития внутри динамического ряда сохранятся и вне этого ряда. Это означает, что основные факторы, сформировавшие выявленную закономерность изменения уровней ряда во времени, сохранятся и в будущем. При составлении прогноза уровней социально – экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. При этом границы интервалов определяются по формуле:
где
При этом среднее квадратическое отклонение тренда рассчитывается по формуле:
где
При экстраполяционном прогнозировании экономической динамики на основе динамических рядов с использованием трендовых моделей выбираются несколько конкурирующих моделей. После выполнения необходимых вычислении производится выбор наилучшей модели тренда. В качестве грубого критерия отбора иногда применяют среднее квадратическое отклонение, вычисленное по формуле (6.16). Выбирается тот тренд, для которого меньше среднее квадратическое отклонение. Проиллюстрируем выравнивание ряда динамики по прямой и по параболе второго порядка. Пример 5. В табл.6.6 представлена динамика производства мяса в регионе. Таблица6.6
Необходимо рассчитать прогноз производства мяса в регионе на 2012год с вероятностью 0, 99, исходя из предположения, что тенденция ряда может быть описана: а) линейной моделью (6.10); б) параболической моделью (6.12). Решение. Расчета коэффициентов нормальных уравнений линейного тренда (6.14) и параболического тренда (6.15) сведем в таблицу 6.7. Таблица 6.7. Расчет параметров систем нормальных уравнений трендовых моделей.
На основании таблицы 6.7 составим нормальные уравнения линейного тренда (6.13), которые имеют вид:
После решения этой системы были получены числовые значения неизвестных параметров:
Теперь необходимо составить систему нормальных уравнений параболического тренда (6.14):
Решение этой системы дает результат: Далее для уравнений параболы (6.12) составим модель параболического тренда:
Аналитическое выравнивание ряда динамики не только делает более чётким направление основной тенденции, но одновременно даёт также числовую её характеристику. В частности, при выравнивании по прямой параметр В дальнейшем необходимо рассчитать выравненные значения уровней для трендовых моделей (6.18) и (6.19). С этой целью в подобранные модели последовательно необходимо подставить текущие номера уровней t. Результаты подсчетов сведем в табл. 6.8. Таблица 6.8 - Расчётная таблица при выравнивании по прямой и по параболе ряда динамики производства мяса в регионе.
После выравнивания уровней динамического ряда посредством двух моделей стало очевидным тенденция к росту производства мясо в регионе. Для выполнения прогноза производства мясо в регионе необходимо рассчитать средние квадратические отклонения каждой модели. Необходимые вычисления сведем в табл. 6.9.
Таблица 6.9 - Расчёт сумм квадратов остаточных отклонений
На основании этой таблицы рассчитаем средние квадратические отклонения моделей: линейный тренд:
тренд параболы:
Так как модель линейной функций имеет меньшую среднеквадратическую ошибку то она и будет использоваться для прогнозирования. Для этого в подобранный модель (6.18) вместо параметра t подставляется время упреждения
Далее по числу степеней свободы
Подставляя сюда рассчитанные величины получим:
Таким образом с вероятностью 0, 99 можно ожидать, что производство мясо в регионе 2012 г. будет не ниже 188, 31 тыс. т., но и не выше 229, 15 тыс. т.
|

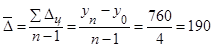 млн. руб.
млн. руб.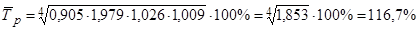 ;
;
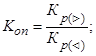
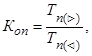 (6.9)
(6.9) максимальный коэффициент роста;
максимальный коэффициент роста;  минимальный коэффициент роста;
минимальный коэффициент роста;  максимальный темп прироста;
максимальный темп прироста;  минимальный темп прироста.
минимальный темп прироста.
 и т.д.
и т.д. .
. - линейная функция;
- линейная функция; - парабола второго порядка;
- парабола второго порядка; - показательная функция.
- показательная функция. ) практически редко сделать на основе одного только содержательного анализа. Обычно на 1-м этапе выбора отбирают функции, пригодные с позиций содержательного анализа, а на 2-м этапе вид функции конкретизируется с помощью иных подходов и приёмов, имеющих эмпирический характер.
) практически редко сделать на основе одного только содержательного анализа. Обычно на 1-м этапе выбора отбирают функции, пригодные с позиций содержательного анализа, а на 2-м этапе вид функции конкретизируется с помощью иных подходов и приёмов, имеющих эмпирический характер. . (6.10)
. (6.10) . (6.11)
. (6.11) . (6.12)
. (6.12) (6.13)
(6.13) фактические,
фактические, 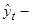 выровненные (расчетные) уровни.
выровненные (расчетные) уровни. и
и  искомой прямой, удовлетворяющие методу наименьших квадратов, находятся путём решения такой системы нормальных уравнений:
искомой прямой, удовлетворяющие методу наименьших квадратов, находятся путём решения такой системы нормальных уравнений: (6.14)
(6.14) и
и  .
.
 , (6.16)
, (6.16) точечный прогноз, рассчитанный по отобранной модели;
точечный прогноз, рассчитанный по отобранной модели; коэффициент доверия по распределению Стьюдента при уровне значимости
коэффициент доверия по распределению Стьюдента при уровне значимости  ;
; среднее квадратическое отклонение тренда.
среднее квадратическое отклонение тренда. , (6.17)
, (6.17) и
и  соответственно фактические и выравненные значения уровней динамического ряда;
соответственно фактические и выравненные значения уровней динамического ряда; число уровней ряда;
число уровней ряда; число определяемых параметров трендовой модели.
число определяемых параметров трендовой модели.
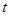


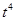



 =160, 73;
=160, 73;  . (6.18)
. (6.18)
 =-0, 26.
=-0, 26. . (6.19)
. (6.19) это абсолютный прирост выровненного уровня за единицу времени
это абсолютный прирост выровненного уровня за единицу времени 



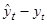

 24, 95;
24, 95; 25, 53.
25, 53. . В результате получим точечный прогноз показателя:
. В результате получим точечный прогноз показателя: 208, 73 тыс. т.
208, 73 тыс. т. и заданной вероятности 0, 99 из специальных таблиц найдем коэффициент доверия к прогнозу. И он равен
и заданной вероятности 0, 99 из специальных таблиц найдем коэффициент доверия к прогнозу. И он равен  . На основании выражения (6.16) запишем границы прогнозируемого показателя:
. На основании выражения (6.16) запишем границы прогнозируемого показателя: .
. .
.


