МЕТОДИЧЕСКИЕ УКАЗАНИЯ И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ. Социально – экономические явления общественной жизни находятся в непрерывном развитии
Социально – экономические явления общественной жизни находятся в непрерывном развитии. Их изменение во времени статистика изучает при помощи построения и анализа рядов динамики. Начиная изучение данной темы, необходимо обратить внимание на классификацию рядов динамики, различия между ними, так как отнесение ряда динамики к тому или иному виду имеет важное значение для их изучения. Выбор соответствующих приёмов и способов анализа определяется характером исходных данных и зависит от задач исследования. Данная тема знакомить студентов с задачами, решение которых дает возможность усвоить правила построения и анализа рядов динамики для характеристики изменения социально – экономических явлений во времени, выявления основной тенденции, закономерностей их развития. Ряд динамики – числовые значения статистического показателя, представленные во временной последовательности. Он состоит из двух граф: в первой указываются периоды (или даты), во второй – показатели, характеризующие изучаемый объект за эти периоды (или на эти даты). Показатели второй графы носят название уровней ряда: первый показатель называется начальным уровнем, последний – конечным. Уровни рядов динамики могут быть выражены абсолютными, средними или относительными величинами. Исходя из этого, ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. Ряды динамики могут быть двух видов: интервальные и моментные. В интервальном ряду приводятся данные, характеризующие величину показателя за определенные периоды (сутки, месяц, квартал, год и т. д.). Особенность интервальных рядов из абсолютных величин является то, что их уровни можно суммировать, получая новые значения объема явления, относящиеся к более длительным периодам. В моментном ряду динамики приводятся данные, характеризующие размеры явления на определенные моменты (даты) времени. Уровни моментных рядов динамики суммировать нельзя; сумма не имеет экономического смысла, так как каждый последующий уровень полностью или частично включает в себя предыдущий уровень. Однако разность уровней имеет смысл, характеризуя увеличение или уменьшение уровня ряда между датами учета. Важнейшим условием правильного формирования рядов динамики является сопоставимость уровней, образующих ряд. Основным требованием сопоставимости уровней является одинаковая методология их исчисления для всех периодов или дат. При этом все уровни должны быть даны не только в одинаковых, но и равноценных единицах измерения. Условием сопоставимости данных является также одинаковая полнота охвата различных частей явления, представленного рядом динамики. Уровни показателей в интервальных динамических рядах должны относиться к периодам с одинаковой продолжительностью. Для моментных рядов должна соблюдаться неизменность даты учета. Вопрос о том, следует ли считать условием сопоставимости данных динамического ряда одинаковость границ территории, к которой относятся данные, решается по – разному. Если ставится задача изучения изменения явления в связи с изменением территории, то в этом случае сопоставляются данные, относящиеся к различной территории. Если же ставится задача изменения темпов развития явления, то сравниваемые показатели должны относиться к неизменной территории. Поэтому, прежде чем анализировать ряд динамики, необходимо обеспечить сопоставимость уровней ряда. Для этого выполняется дополнительные расчеты, которые называются смыканием уровней динамических рядов. Условием же сопоставимости уровней интервального временного ряда является равенство периодов, за которые приводятся данные. Если это условие нарушено, то исследуемый ряд подвергают дополнительной обработке - рассчитывают уровни ряда в среднем на единицу времени. Пример 1. Объем инвестиций по фирме характеризуется следующими данными (табл. 6.1). Таблица 6.1
Уровни представленного ряда не сопоставимы между собой, так как показатели относятся к периодам с различной продолжительностью. Для того, чтобы выявить изменение динамики капитальных вложений во времени, необходимо определить величину капитальных вложений на одну и ту же единицу каждого периода – один год. Объем капитальных вложений за один год составляет (млн. руб.): 1994 – 1999 гг. – 228, 16 (1140, 8: 5); 2000 – 2003 гг. – 408, 50 (1225, 5: 3); 2004 – 2010 гг. – 493, 43 (2960, 6: 6); 2010 г. – 508, 80. Из анализа полученных данных видно, что объем капитальных вложений по фирме за период 1994 – 2011 гг. имеет тренд к повышению. Если несопоставимость в рядах динамики вызвана административно - территориальными изменениями, то для изучения развития явления необходимо построить ряд сопоставимых уровней в новых территориальных границах.
Пример2. Имеются данные, характеризующие общий объём продукции промышленности в одном из регионов (в фактически действовавших ценах), млрд. руб.: Таблица 6.2
Для приведения этой информации к сопоставимому виду для определяется коэффициент пересчета (коэффициент соотношения двух уровней):
Умножая на этот коэффициент уровни продукции 2005, 2006 и 2007 гг. и объединив их с уровнями в новых границах можно построит ряд динамики сопоставимых уровней в новых территориальных условиях региона (табл. 6.3). Таблица 6.3
Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени. Для выявления специфики развития изучаемых явлений за отдельные периоды времени определяют абсолютные и относительные показатели изменения ряда в динамики: абсолютные приросты, абсолютное значение одного процента прироста, темп роста и прироста. Выяснение сущности этих показателей, их взаимосвязей, методов расчёта – необходимое условие усвоения данной темы. Рассматривая данные показатели, необходимо правильно выбрать базу сравнения, которая зависит от цели исследования. При сравнении каждого уровня ряда с предыдущим получаются цепные показатели; при сравнении каждого уровня с одним и тем же уровнем (базой) получают базисные показатели динамики. Пример 3. Требуется провести анализ динамики реализации продукции фирмы за 2010-2011 гг. Для удобства и наглядности исходные и рассчитанные показатели изложены в табличной форме (таблица 6.4). Таблица 6.4 – Динамика реализации продукции фирмы за 2007-2011 гг. и расчет аналитических показателей динамики
Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель – абсолютный прирост (
где
Например, абсолютное уменьшение реализации продукции фирмы за 2008 г. по сравнению с 2007 г. составило: 806 – 891 = -85 млн. руб. (таблица 6.1, гр. 2), а по сравнению с базисным (2007 г.) реализация продукции в 2011 г. возросла на 760 млн. руб. (гр. 3). Интенсивность изменения уровня ряда динамики оценивается отношением текущего уровня к предыдущему или базисному, которая всегда представляет собой положительное число. Этот показатель принято называть темпом роста (
Так, для 2011 г. темп роста по сравнению с 2007 г. составил
В некоторых случаях интенсивность изменения уровней оценивается коэффициентом роста, который показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если это коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Цепной и базисный коэффициенты роста рассчитываются по формулам соответственно:
Для выражения изменения величины абсолютного прироста уровня ряда динамики в относительных величинах определяется темп прироста (
Темп прироста может быть вычислен также путем вычитания из темпов роста 100%, т.е. В нашем примере (таблица 6.1, гр. 6, 7) он показывает, например, на сколько процентов реализация продукции в 2011 г. снизилась (возросла) по сравнению с 2007 г.: Показатель абсолютного значения 1% прироста ( Для 2011 г. абсолютное значение 1% прироста (таблица 6.1, гр. 8) равно: Особое внимание следует уделять методам расчета средних показателей рядов динамики, которые являются обобщающей характеристикой его абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики. Различают следующие средние показатели: - средний уровень ряда динамики; - средний абсолютный прирост; - средний темп роста; - средний темп прироста. Методы расчета среднего уровня интервального и моментного рядов динамики различны. Для интервальных рядов динамики средний уровень за исследуемый период времени определяется по формуле средней арифметической: при равных интервалах применяется средняя арифметическая простая:
при неравных интервалах – средняя арифметическая взвешенная:
где Обобщающий показатель скорости изменения уровней во времени - абсолютный прирост (убыль), представляющий собой обобщающую характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряда лет можно рассчитать средний годовой абсолютный прирост как среднюю арифметическую простую:
где Сводной обобщающей характеристикой интенсивности изменения уровней динамического ряда служит средний темп роста (снижения), показывающий во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах
где m - число цепных коэффициентов роста. Если известны уровни динамического ряда, то формула для расчета среднего коэффициента роста принимает вид:
где
Рассчитаем средний уровень для нашего примера. Так как анализируем интервальный ряд динамики с равноотстоящими уровнями во времени, то средний уровень рассчитаем по формуле (6.4):
|


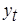




 ). Его величина определяется как разность двух сравниваемых уровней. Она вычисляется по формуле:
). Его величина определяется как разность двух сравниваемых уровней. Она вычисляется по формуле: , (6.1)
, (6.1) - уровень i -го года;
- уровень i -го года; - уровень базисного года.
- уровень базисного года.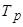 ). Он выражается в процентах, т.е.:
). Он выражается в процентах, т.е.: или
или  . (6.2)
. (6.2)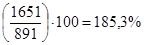 (таблица 6.1, гр. 2).
(таблица 6.1, гр. 2). , или
, или  . (6.3)
. (6.3) ), который рассчитывается как отношение абсолютного прироста к предыдущему или базисному уровню, т.е.:
), который рассчитывается как отношение абсолютного прироста к предыдущему или базисному уровню, т.е.: , или
, или  . (6.4)
. (6.4) .
. или
или  .
. ) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в %, т.е.:
) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в %, т.е.:  или
или  . Расчет этого показателя имеет экономический смысл только на цепной основе.
. Расчет этого показателя имеет экономический смысл только на цепной основе. или
или  млн. руб.
млн. руб. ; (6.4)
; (6.4) ; (6.5)
; (6.5) веса, длительность интервалов времени между смежными датами.
веса, длительность интервалов времени между смежными датами. , (6.6)
, (6.6)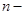 число уровней в динамическом ряду.
число уровней в динамическом ряду. , то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):
, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»): , (6.7)
, (6.7) 100%, (6.8)
100%, (6.8) .
.


