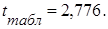МЕТОДИЧЕСКИЕ УКАЗАНИЯ И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ. Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет в развитии экономики значительную роль
Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет в развитии экономики значительную роль. Оно позволяет глубже понять сложный механизм причинно-следственных отношений. В настоящее время важно уметь количественно измерить тесноту причинно-следственных связей и выявить форму связи между экономическими процессами. Для исследования интенсивности, вида и формы причинных связей широко применяется корреляционный и регрессионный анализ. Выявление количественных соотношений дает возможность лучше понять природу исследуемого явления. Это, в свою очередь, позволяет воздействовать на изученные факторы, вмешиваться в соответствующий процесс с целью получения нужных результатов. Но, чтобы глубоко и основательно проникнуть в суть явления, необходимо исследовать и раскрыть его причинные связи, его отношения с другими явлениями. Под причинной связью понимают такую связь, когда изменение одних процессов есть следствие изменения других. Обычно одно и то же экономическое явление выступает как результат, следствие, эффект одной или нескольких причин. Вместе с тем оно служит причиной наступления других явлений или процессов. Раскрытие объективно существующих причинных зависимостей приводит исследователя к источнику зарождения отдельных процессов. Признание факта множественности причин и следствий в реальной действительности нашло свое отражение и при исследовании закономерностей в экономике. Так, на величину себестоимости единицы продукции влияют объем производства, используемая технология и уровень производительности труда. Производительность труда, которая служит причиной формирования себестоимости, в свою очередь является следствием таких причин, как уровень развития техники и подготовки работников, эффективность использования парка оборудования и т. д. Урожайность сельскохозяйственных культур зависит от состояния почвы, состава и количества внесенных удобрений, метеорологических условий и других не менее важных причин. Один из важных признаков причинной связи - это соблюдение временной последовательности причины и следствия. Причина всегда предшествует следствию. Однако не всякое предшествующее событие служит подлинной причиной появления последующего. Поэтому для правильного понимания причинно-следственных отношений большую опасность представляют совпадения явлений и одновременно развивающиеся процессы. Например, увеличение числа онкологических заболеваний за последние 10 лет ни в коей мере не является причиной спада промышленного производства за тот же период времени. Следует также отметить, что статистический анализ требует такого обязательного условия, как повторяемость явления. Ведь только наличие достаточно большого числа наблюдений обеспечивает практическую возможность выявления связи. Это обусловлено тем, что причинному действию и определяемому им следствию присуща в той или иной степени случайность. Большинство экономических процессов представляют собой результат множества одновременно действующих причин. Каждый процесс при повторении его причинного комплекса за счет случайности реализуется с отклонением от закона, лежащего в его основе. Различают два вида зависимости между экономическими явлениями: функциональную и статистическую. Зависимость между двумя величинами Однако гораздо чаще в экономике имеет место не функциональная, а статистическая зависимость, когда каждому фиксированному значению независимой переменой X соответствует не одно, а множество значений зависимой переменной Y, причем заранее нельзя сказать, какое именно значение примет Y. Это связано с тем, что на Y кроме переменной X влияют и многочисленные неконтролируемые случайные факторы. В этой ситуации Y является случайной величиной, а переменная X может быть как детерминированной, так и случайной величиной. Частным случаем статистической зависимости является корреляционная зависимость, при которой функциональной зависимостью связаны фактор X и среднее значение (математическое ожидание) результативного показателя Y. Статистическая зависимость может быть выявлена лишь по результатам достаточно большого числа наблюдений. Графически статистическая зависимость двух признаков может быть представлена с помощью поля корреляции, при построении которого на оси абсцисс откладывается значение факторного признака X, а по оси ординат - результирующего Y. В качестве примера на рис. 7.1 представлены данные, иллюстрирующие прямую зависимость между х и у (рис. 7.1, a) и обратную зависимость (рис. 7.1, б). В случае «а» это прямая зависимость между, к примеру, среднедушевым доходом (х) и сбережением (у) в семье. В случае «б» речь идет об обратной зависимости. Такова, например, зависимость между производительностью труда (х) и себестоимостью единицы продукции (у).
y
x x а б
Рис. 7.1. Поле корреляции На рис. 7.1 каждая точка характеризует объект наблюдения со своими значениями х и у. На рис. 7.1 также представлены прямые линии, линейные уравнения регрессии типа Ставя задачу статистического исследования зависимостей, важно хорошо представлять конечную прикладную цель построения моделей статистической зависимости между результативным показателем у с одной стороны и объясняющими переменными Первая из них состоит в установлении самого факта наличия (или отсутствия) статистически значимой связи между У и X. При такой постановке задачи статистический вывод имеет альтернативную природу - «связь есть» или «связи нет». Он обычно сопровождается лишь численной характеристикой - измерителем степени тесноты исследуемой зависимости. Задача оценки степени тесноты связи между показателями решается методами корреляционного анализа. При этом выбор формы связи между результативным показателем у и объясняющими переменными Вторая цель сводится к прогнозу, восстановлению неизвестных индивидуальных или средних значений результативного показателя «y» по заданным значениям объясняющих переменных. Задача восстановления средних значений результативного показателя «у» по заданным значениям объясняющих переменных решается методами регрессионного анализа. При этом выбор формы и вида зависимости «у» от объясняющих переменных Таким образом, в задачах исследования зависимостей используются методы корреляционного и регрессионного анализов. При этом методы корреляционного анализа применяют на этапе предварительной обработки информации, результаты которого используют в регрессионном анализе при построении и анализе свойств уравнения регрессии. Выбор тех или иных методов анализа во многом определяется природой изучаемых переменных, шкалой в которой они измерены. Количественные переменные позволяют измерять степень проявления изучаемого свойства объекта (денежный доход и сбережения семьи, объем валовой продукции, численность работников на предприятии и т. п.). Порядковые (или ординальные) переменные позволяют упорядочивать анализируемые объекты по степени проявления в них изучаемого свойства (уровень жилищных условий семьи, квалификационный разряд рабочего, уровень образования работника и т. п.). Наконец, классификационные (или номинальные)переменные дают возможность разбивать обследованную совокупность объектов на не поддающиеся упорядочиванию однородные классы (профессия работника, мотив миграции семьи, отрасль промышленности и т. п.). Теперь рассмотрим приемы и методы, позволяющие установить наличие связи между исследуемыми переменными, выявить структуру этих связей и измерить их тесноту. Поскольку перечисленные задачи решаются с помощью вычисления и анализа соответствующих корреляционных характеристик, совокупность используемых для этих целей методов называют корреляционным анализом. Корреляционный анализ разработан К. Пирсоном и Дж. Юлом. Он призван прежде всего ответить на вопрос, как выбрать с учетом специфики и природы анализируемых переменных подходящий измеритель статистической связи ( коэффициент корреляции, корреляционное отношение, ранговый коэффициент корреляции и т. д.) Далее предстоит решить задачу, как оценить его числовые значения по имеющимся выборочным данным. Корреляционный анализ позволяет найти методы проверки того, что полученное числовое значение анализируемого измерителя связи действительно свидетельствует о наличии статистической связи. Наконец, он помогает определить структуру связей между исследуемыми k признаками Корреляционный анализ количественных признаков. Одним из основных показателей взаимозависимости двух случайных величин является парный коэффициент корреляции, служащий мерой линейной статистической зависимости между двумя величинами. Этот показатель соответствует своему прямому назначению, когда статистическая связь между соответствующими признаками в генеральной совокупности линейна. То же самое относится к частным и множественным коэффициентам корреляции. Парный коэффициент корреляции, характеризующий тесноту связи между случайными величинами х и у, определяется по формуле:
где Парный коэффициент корреляции изменяется в пределах от -1 до +1, то есть -1 < Содержательная интерпретация коэффициента корреляции приведена в табл. 7.1. Таблица 7.1 Содержательная интерпретация коэффициента корреляции
Коэффициент корреляции, определяемый (7.1), относится к генеральной совокупности и как всякий параметр генеральной совокупности нам не известен. Его можно лишь оценить по результатам выборочных наблюдений. Выборочный парный коэффициент корреляции, найденный по выборке объемом п, где
где
Формула (7.2) симметрична, т.е. r ху= rух =r. Если в ее числителе раскрыть скобки, то после несложных преобразований получим формулу, которую широко используют при вычислении коэффициента корреляции.
где
Выборочный коэффициент корреляции r, как всякая выборочная характеристика, является случайной величиной, и по отдельным его значениям нельзя делать окончательные выводы о степени тесноты линейной связи между двумя величинами. Здесь речь может идти о некоторых практических, качественных рекомендациях (табл. 7.2) при достаточно больших n (n > 40). В табл. 7.2 значения rрассматриваются по модулю, так как степень тесноты связи зависит от близости rк единице без учета знака. Таблица 7.2. Качественные характеристики связи
Степень зависимости между х и у существенно выше в случае, когда r= -0, 8 по сравнению со случаем когда r = 0, 5. Оценка существенности линейного коэффициент корреляции при большом объеме выборки (свыше 500) проводится с использованием отношения коэффициента корреляции (
где Если это отношение окажется больше значения t – критерия Стьюдента, определяемого по специальным таблицам теории вероятностей, то коэффициент корреляции значимо отличается от нуля. При недостаточном большом объеме выборки величину средней квадратической ошибки коэффициента корреляции определяют по формуле:
В этом случае:
Полученные значения В тех случаях, когда Средняя квадратическая ошибка Z – распределения зависит только от объема выборки и определяется по формуле:
По таблице соотношений между Если соотношения В практических исследованиях могут быть использованы и другие показатели для определения степени тесноты связи. Элементарной характеристикой степени тесноты связи является коэффициент Фехнера:
где Коэффициент Фехнера целесообразно использовать для установления факта наличия связи при небольшом объеме исходной информации. Он изменяется в пределах
Для определения тесноты связи как между количественными, так и между качественными признаками, при условии, что значения этих признаков могут быть проранжированы по степени убывания или возрастания, используется ранговый коэффициент корреляции Спирмена:
где Он варьирует в пределах от – 1, 0 до + 1, 0. Ранговый коэффициент корреляции Спирмена обычно исчисляется на основе небольшого объема исходной информации, поэтому необходимо выполнить проверку его существенности. В приложении 7 приводится таблица предельных значений коэффициента корреляции рангов Спирмена при условии верности нулевой гипотезы об отсутствии корреляционной связи при заданном уровне значимости и определенном объеме выборочных данных. Если полученное значение Для исследования степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, может быть использован коэффициент ассоциации Д. Юла или коэффициент контингенции К. Пирсона. Расчетная таблица в этом случае состоит из четырех ячеек («таблица четырех полей»), статистическое сказуемое которой схематически может быть представлено в следующем виде:
В расчетной таблице: a, b, c, d – частоты взаимного сочетания (комбинации) двух альтернативных признаков – A – Коэффициент ассоциации исчисляется по формуле:
Коэффициент контингенции:
где Коэффициент контингенции также изменяется от – 1, 0 до + 1, 0, но всегда его величина для тех же данных меньше коэффициента ассоциации. Рассмотрим теперь на примере трехмерной генеральной совокупности ( В этом случае выборка объемом п будет представлять собой матрицу наблюдений х:
В ней каждая i-я строка (i = 1, 2,..., n)характеризует i -и экономический объект, а столбец, например первый, содержит значение для 1-го показателя для всех п объектов. По данным первого столбца матрицы X можно определить среднее значение
Аналогичным образом определяются выборочные характеристики Отсюда, согласно (7.4), рассчитаем выборочные парные коэффициенты корреляции Частный коэффициент корреляции ρ 12/3 характеризует степень линейной зависимости между двумя величинами, например Выборочный частный коэффициент корреляции, как выборочный аналог определяется по формуле:
где В трехмерной модели имеются еще два частных коэффициента корреляции r12/3 и r23/1 которые рассчитываются аналогично. Мы имеем два коэффициента корреляции: парный r12 и частный r12/3которые характеризуют степень линейной зависимости между величинами Таким образом, частный коэффициент корреляции более точно характеризует степень линейной зависимости. Частный коэффициент корреляции обладает всеми свойствами парного, т.е. изменяется в пределах от-1 до+1. Если частный коэффициент корреляции равен ±1, то связь между двумя величинами функциональная, а равенство его нулю свидетельствует о линейной независимости этих величин. Множественный коэффициент корреляции, например ρ 12/3, характеризует степень линейной зависимости между величиной Выборочный множественный коэффициент корреляции, выборочный аналог генерального коэффициента ρ 1/23, можно выразить через парные коэффициенты:
В трехмерной модели имеются еще два множественных коэффициента корреляции r2/13 и r3/12, которые рассчитываются аналогично. Квадрат коэффициента корреляции называют коэффициентом детерминации. При этом множественный коэффициент детерминации, например r1/23, характеризует долю дисперсии Таким образом, коэффициент детерминации характеризует долю дисперсии одной величины, например у, объясняемой влиянием фактора Методы регрессионного анализа. После того как с помощью корреляционного анализа выявлено наличие статистических связей между переменными и оценена степень их тесноты, обычно переходя к математическому описанию конкретного вида зависимостей с использованием регрессионного анализа. С этой целью подбирают класс функций, связывающий результативный показатель у и аргументы Функция Для точного описания уравнения регрессии необходимо знать закон распределения результативного показателя у. В статистической практике обычно приходится ограничиваться поиском подходящих аппроксимаций для неизвестной истинной функции регрессии Рассмотрим взаимоотношение между истинной
где ε - случайная величина, имеющая нормальный закон распределения, причем Mε =0 и Dε =σ 2. Истинная функция регрессии в этом случае имеет вид: Предположим, что точный вид истинного уравнения регрессии нам не известен, но мы располагаем девятью наблюдениями над двумерной случайной величиной, связанной соотношением
у 70-60-50-40-30-20- 10-
Рис. 7.2. Взаимное расположение истинной f(x) и теоретической Расположение точек на рис. 7.2 позволяет ограничиться классом линейных зависимостей вида: Поскольку мы ошиблись в выборе класса функции регрессии, а это достаточно часто встречается в практике статистических исследований, то наши статистические выводы и оценки окажутся ошибочными. И как бы мы ни увеличивали объем наблюдений, наша выборочная оценка Тип модели выбирается на основе сочетания теоретического анализа и исследования эмпирических данных посредством построения эмпирической линии регрессии. Чаще других встречаются следующие виды уравнений регрессии: а) линейная функция:
б) гиперболическая функция:
в) параболическая функция:
г) показательная функция:
д) степенная функция:
е) линейная многомерная функция:
Для определения численных значений параметров уравнения связи (линии регрессии) используется метод наименьших квадратов и решается система нормальных уравнений. Применение метода наименьших квадратов к линейной функции (7.16) дает нам систему нормальных уравнении:
Применив метод наименьших квадратов к функции гиперболы (7.17) переходят к системе нормальных уравнений:
Для определения параметров параболы второго порядка система нормальных уравнений такова:
Прежде чем применить метод наименьших квадратов к показательной и степенной функциям их приводят к линейному виду путем логарифмирования. Далее применяют метод наименьших квадратов и переходят к системе нормальных уравнении.
Пример 7.1. На основании выборочных данных (табл. 7.3) о деятельности п = 6 коммерческих фирм оценить тесноту связи между прибылью (млн руб.) (у)и затратами на 1 руб. произведенной продукции (х). Таблица 7.3. Исходные и расчетные данные для определения r
Используем формулу (7.4): Тогда Следовательно, между прибылью ( Средняя квадратическая ошибка коэффициента корреляции рассчитаем по формуле (7.7):
Необходимо получить по формуле (7.8) расчетный коэффициент Стьюдента:
По таблице приложения 6 найдем табличное значение критерия Стьюдента при P=0, 95 и k=6-2; Так как
|

 отображающими соответственно два явления, называется функциональной, если каждому значению величины X соответствует единственное значение величины Y и наоборот. Примером функциональной связи в экономике может служить зависимость производительности труда от объема произведенной продукции и затрат рабочего времени. При этом следует отметить, что если Х- детерминированная, не случайная величина, то и функционально зависящая от нее величина У тоже является детерминированной. Если же Х- величина случайная, то и Y также случайная величина.
отображающими соответственно два явления, называется функциональной, если каждому значению величины X соответствует единственное значение величины Y и наоборот. Примером функциональной связи в экономике может служить зависимость производительности труда от объема произведенной продукции и затрат рабочего времени. При этом следует отметить, что если Х- детерминированная, не случайная величина, то и функционально зависящая от нее величина У тоже является детерминированной. Если же Х- величина случайная, то и Y также случайная величина.




 , характеризующие функциональную зависимость между независимой переменной
, характеризующие функциональную зависимость между независимой переменной  и средним значением результативного показателя у. Таким образом, по уравнению регрессии, зная х, можно восстановить лишь среднее значение у.
и средним значением результативного показателя у. Таким образом, по уравнению регрессии, зная х, можно восстановить лишь среднее значение у. , с другой (до сих пор рассматривалась только одна объясняющая переменная х). Отметим две основных цели подобных исследований.
, с другой (до сих пор рассматривалась только одна объясняющая переменная х). Отметим две основных цели подобных исследований. , а также выбор состава последних играет вспомогательную роль, призванную максимизировать характеристику степени тесноты связи.
, а также выбор состава последних играет вспомогательную роль, призванную максимизировать характеристику степени тесноты связи. нацелен на минимизацию суммарной ошибки, т. е. отклонений наблюдаемых значений у от значений, полученных по регрессионной модели.
нацелен на минимизацию суммарной ошибки, т. е. отклонений наблюдаемых значений у от значений, полученных по регрессионной модели. , сопоставив каждой паре признаков ответ («связь есть» или «связи нет»).
, сопоставив каждой паре признаков ответ («связь есть» или «связи нет»). (7.1)
(7.1) и
и  -математические ожидания величин х и у, а
-математические ожидания величин х и у, а  их среднеквадратические отклонения.
их среднеквадратические отклонения. < +1. При этом между величинами х и у связь функциональная (прямая - при
< +1. При этом между величинами х и у связь функциональная (прямая - при 
 результат i-го наблюдения i = 1, 2,..., п, определяется по формуле:
результат i-го наблюдения i = 1, 2,..., п, определяется по формуле: (7.2)
(7.2) ;
;  , a
, a 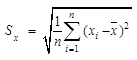 ;
;  (7.3)
(7.3)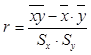 (7.4)
(7.4) - средняя арифметическая произведения двух величин, т. е.
- средняя арифметическая произведения двух величин, т. е. (7.5)
(7.5)
 ) к его средней квадратической ошибке
) к его средней квадратической ошибке 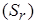 :
: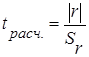 , (7.6)
, (7.6) .
. . (7.7)
. (7.7) . (7.8)
. (7.8) сравнивается с табличным значением t – критерия Стьюдента.
сравнивается с табличным значением t – критерия Стьюдента. . (7, 9)
. (7, 9) и
и  (приложение 9)находят значение
(приложение 9)находят значение  ) окажется больше табличного значения критерия Стьюдента при определенном уровне значимости, то можно говорить о наличии связи между признаками в генеральной совокупности.
) окажется больше табличного значения критерия Стьюдента при определенном уровне значимости, то можно говорить о наличии связи между признаками в генеральной совокупности. , (7.10)
, (7.10)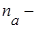 количество совпадений знаков отклонений индивидуальных величин факторного признака
количество совпадений знаков отклонений индивидуальных величин факторного признака  и результативного признака
и результативного признака 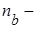 количество несовпадений знаков отклонений индивидуальных значений изучаемых признаков от значения их средней арифметической.
количество несовпадений знаков отклонений индивидуальных значений изучаемых признаков от значения их средней арифметической.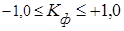 .
. , (7.11)
, (7.11) разность между величинами рангов признака – фактора и результативного признака;
разность между величинами рангов признака – фактора и результативного признака;  число показателей (рангов) изучаемого ряда.
число показателей (рангов) изучаемого ряда. превышает критическую величину при данном уровне значимости, то нулевая гипотеза может быть отвергнута, т. е. величина
превышает критическую величину при данном уровне значимости, то нулевая гипотеза может быть отвергнута, т. е. величина  (нет)
(нет)
 (нет)
(нет)
 . (7.12)
. (7.12) , (7.13)
, (7.13) ,
,  ,
,  ,
,  числа в четырехклеточной таблице.
числа в четырехклеточной таблице. ) понятия и правила вычисления частных и множественных коэффициентов корреляции. Пусть каждый экономический объект, элемент генеральной совокупности характеризуется тремя показателями
) понятия и правила вычисления частных и множественных коэффициентов корреляции. Пусть каждый экономический объект, элемент генеральной совокупности характеризуется тремя показателями  . Требуется по данным выборки объемом п из генеральной совокупности исследовать взаимосвязь между этими показателями.
. Требуется по данным выборки объемом п из генеральной совокупности исследовать взаимосвязь между этими показателями.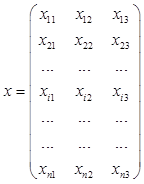
 , и выборочную дисперсию S12, первого показателя.
, и выборочную дисперсию S12, первого показателя. ;
; 
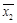 ,
,  и
и  ,
,  .
.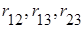 .
.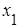 и
и 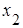 при исключенном влиянии остальных величин, включенных в модель (в нашем случае - это
при исключенном влиянии остальных величин, включенных в модель (в нашем случае - это 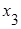 ).
). , (7.14)
, (7.14)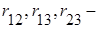 выборочные парные коэффициенты корреляции.
выборочные парные коэффициенты корреляции. .Однако если парный коэффициент r12 оценивает степень зависимости на фоне влияния
.Однако если парный коэффициент r12 оценивает степень зависимости на фоне влияния  (7.15)
(7.15) = 0, 85, то это свидетельствует, что 85% дисперсии
= 0, 85, то это свидетельствует, что 85% дисперсии  , отбирают наиболее информативные аргументы, вычисляют оценки неизвестных значений параметров уравнения связи и анализируют свойства полученного уравнения.
, отбирают наиболее информативные аргументы, вычисляют оценки неизвестных значений параметров уравнения связи и анализируют свойства полученного уравнения. , описывающая зависимость среднего значения результативного признака у от заданных значений аргументов, называется функцией (уравнением) регрессии. Термин «регрессия» (лат. - отступление, возврат к чему-либо) введен английским психологом и антропологом Ф. Гальтоном и связан исключительно со спецификой одного из первых конкретных примеров, в котором это понятие было использовано. Так, обрабатывая статистические данные в связи с анализом наследственности роста, Ф. Гальтон нашел, что если отцы отклоняются от среднего роста всех отцов на х дюймов, то их сыновья отклоняются от среднего роста всех сыновей меньше, чем на х дюймов. Выявленная тенденция была названа «регрессией к среднему состоянию». Стех пор термин «регрессия» широко используется в статистической литературе, хотя во многих случаях он недостаточно точно характеризует понятие статистической зависимости.
, описывающая зависимость среднего значения результативного признака у от заданных значений аргументов, называется функцией (уравнением) регрессии. Термин «регрессия» (лат. - отступление, возврат к чему-либо) введен английским психологом и антропологом Ф. Гальтоном и связан исключительно со спецификой одного из первых конкретных примеров, в котором это понятие было использовано. Так, обрабатывая статистические данные в связи с анализом наследственности роста, Ф. Гальтон нашел, что если отцы отклоняются от среднего роста всех отцов на х дюймов, то их сыновья отклоняются от среднего роста всех сыновей меньше, чем на х дюймов. Выявленная тенденция была названа «регрессией к среднему состоянию». Стех пор термин «регрессия» широко используется в статистической литературе, хотя во многих случаях он недостаточно точно характеризует понятие статистической зависимости.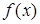 , так как исследователь не располагает точным знанием условного закона распределения вероятностей анализируемого результирующего показателя у при заданных значениях аргумента х.
, так как исследователь не располагает точным знанием условного закона распределения вероятностей анализируемого результирующего показателя у при заданных значениях аргумента х. , модельной регрессией
, модельной регрессией  и оценкой
и оценкой  регрессии. Пусть результативный показатель у связан с аргументом х соотношением:
регрессии. Пусть результативный показатель у связан с аргументом х соотношением: ,
, =
=  .
.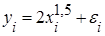 и представленной на рис. 7.2.
и представленной на рис. 7.2.

 О | 2 | 4 | 6 |8 | 10 x
О | 2 | 4 | 6 |8 | 10 x +
+ 
 ; (7.17)
; (7.17) ; (7.18)
; (7.18) ; (7.19)
; (7.19) ; (7.20)
; (7.20) . (7.21)
. (7.21) . (7.22)
. (7.22)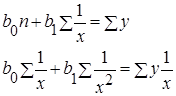 . (7.23)
. (7.23)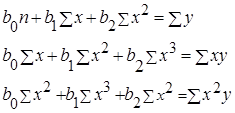 . (7.24)
. (7.24)

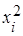

 Прежде всего определим Sx и Sy:
Прежде всего определим Sx и Sy:  ;
; 

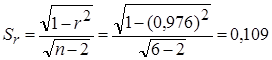 .
. .
.