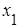ЗАДАЧИ И УПРАЖНЕНИЯ. 7.1. В мартеновском цехе завода произведены испытания для определения зависимости производительности печи от содержания углерода в металле
7.1. В мартеновском цехе завода произведены испытания для определения зависимости производительности печи от содержания углерода в металле. Результаты следующие (табл. 7.1). Таблица 7.1
На основе приведённых данных требуется: 1) проверить первичную информацию по признаку-фактору на однородности; 2) установить факт наличия связи с помощью аналитической группировки; 3) с помощью линейного коэффициента корреляции измерить степень тесноты связи; оценить существенность полученного значения коэффициента корреляции с помощью t-критерия Стьюдента при вероятности 0, 95; 4) определить модель линейной зависимости, оценить её достоверность. 7.2. Имеются следующие данные о производительность труда рабочих, выполняющих одинаковую операцию по обработке детали № 408 (табл. 7.2). Таблица 7.2
Определить степень тесноты связи между уровнем производительности труда рабочих и стажем их работы. 7.3. Для выявления зависимости производительности труда рабочих, выполняющих в цехе одинаковую операцию по обработке деталей № 312, от стажа их работы был найден линейный коэффициент корреляции, равный 0, 80. Кроме того, известны такие данные: 1) средний стаж работы рабочих – х̅ =5 лет; 2) среднее квадратическое отклонение по стажу – σ х=2 года; 3) среднее квадратическое отклонение по производительности труда – σ у=4, 4 шт. (число обработанных деталей); 4) коэффициент вариации по производительности труда – υ у=40, 0%. Найти аналитическое уравнение связи, характеризующее зависимость производительности труда рабочих от стажа их работы. 7.4. Для определения степени влияния стоимости основного капитала на выпуск продукции по 20 предприятиям рассчитаны следующие показатели: а) линейный коэффициент корреляции, равный 0, 8; б) эмпирическое корреляционное отношение, равное 0, 84. Возможно ли в качестве уравнения связи использовать функцию вида у=а+bх? 7.5. Для оценки степени тесноты связи между уровнем выработки рабочих и стажем их непрерывной работы была рассчитана величина корреляционного отношения, оказавшаяся равной 0, 9 (объём выборки был равен 100). Определить величину средней внутригрупповой дисперсии, если известно, что общая дисперсия выработки рабочих составляет 6, 6. 7.6. В табл. 7.3 представлены следующие данные. Таблица 7.3
Определить степень тесноты связи между стажем работы и размером заработной платы рабочих. 7.7. По 20 однородным предприятиям была получена модель, отражающая зависимость выпуска продукции (у) за месяц от размера основного капитала (х): у=12, 0+0, 5х. Кроме того, по этой совокупности предприятий известны следующие данные: а) средняя стоимость основного капитала на одно предприятие - х̅ =12, 0 млн. руб.; б) средний размер выпуска продукции на одно предприятие у̅ =18, 0 млн. руб.; в) среднее квадратическое отклонение по стоимости основного капитала – σ х=3, 5 млн. руб.; Г) среднее квадратическое отклонение по размеру выпуска продукции – σ у=2, 0 млн. руб. Определить степень тесноты связи между размером выпуска продукции и стоимостью основного капитала, учитывая форму связи и используя для этого необходимые данные, из числа приведённых выше. 7.8. В результате обследования студентов экономического факультета института получены следующие данные (табл. 7.4). Таблица 7.4
Определить коэффициент контингенции между успеваемостью спортивных секций. 7.9. По результатам социологического обследования получены следующие данные (табл. 7.5). Таблица 7.5
Определить коэффициент ассоциации и контингенции между удовлетворённостью работой и полом. 7.10. Имеются следующие данные по 20 предприятиям городского хозяйства об объёме продукции (услуг) за месяц и уровне механизации труда (табл. 7.6). Требуется по приведённым данным для выявления наличия связи между объёмом продукции и уровнем механизации труда: 1) построить аналитическую таблицу и дать графическое изображение линии связи; 2) измерить тесноту связи между признаками с помощью коэффициента корреляции рангов; проверить его достоверность.
Таблица 7.6
7.11. Составить линейное уравнение регрессии, если известно, что а=2, 8; линейный коэффициент корреляции r=0, 9; дисперсии признаков х и у соответственно равны 25 и 36. 7.12. По группе однородных предприятий для построения многофакторной модели, отражающей зависимость уровня годовой производительности труда работников, получена следующая матрица парных коэффициентов корреляции (табл. 7.7). Таблица 7.7
В табл. 7.7: Y – годовая производительность труда работников; X1 – вооружённость труда основными средствами; X2 – удельный вес производительности оборудования в общей стоимости основных средств; X3 – энерговооружённость труда; X4 – коэффициент загрузки оборудования. Требуется на основе анализа матрицы парных коэффициентов корреляции указать факторы, которые следуют включить в многофакторную модель производительности труда. 7.13. По предприятиям имеются следующие данные о ёмкости электросталеплавильных печей (т) и расходе электроэнергии на 1 т выплавленной стали 9кВт*ч/т) (табл. 7.8). Таблица 7.8
По приведённым данным требуется: 1) проверить первичную информацию на однородность и нормальность распределения; 2)построить аналитическую таблицу для выявления зависимости расхода электроэнергии от ёмкости печи; 3) дать графическое изображение связи; 4) измерить степень тесноты связи с помощью корреляционного отношения; 5) рассчитать параметры линейного уравнения связи и его среднюю квадратическую ошибки. 7.14. По 100 однородным предприятиям было получено уравнение, характеризующее зависимость себестоимости продукции (y) от уровня производительности труда работников (x):
Кроме того, по этой же совокупности предприятий известны следующие данные: А) где y̅ - средняя себестоимость продукции по всем предприятиям; Б) где х̅ - средний уровень производительности труда по всем предприятиям; В) где
Определить степень тесноты связи между себестоимостью продукции и уровнем производительности труда, учитывая форму связи и используя для этого необходимые данные из числа приведённых выше. Сформулировать вывод. 7.15. Распределение грузовых автотранспортных предприятий города по формам собственности и уровню рентабельности следующее (табл. 7.9). Таблица 7.9
Требуется для оценки влияния формы собственности на уровень рентабельности определить коэффициент взаимной сопряжённости К. Пирсона и А.А. Чупрова. Сформулировать вывод. 7.16. Ниже приведены экспериментальные данные исследования ковкого чугуна от его химического состава (табл. 7.10). На основе приведённых данных требуется: 1) проверить первичную информацию по признаку-фактору на однородность и нормальность распределения; 2) исключить из первичной информации резко выделяющихся анализ, в котором признак-фактор не попадает в интервал x̅ + 3σ х; 3) построить аналитическую таблицу для установления факта наличия связи; 4) по данным аналитической группировки построить график эмпирической линии связи; 5) измерить степень тесноты связи при помощи линейного коэффициента корреляции, оценив его существенность с помощью t-критерия Стьюдента при вероятности 0, 954; 6) определить модель линейной зависимости, оценив её достоверность. Таблица 7.10
7.17. Имеются следующие данные о колеблемости пробега автобусов одной модели до капитального ремонта (табл. 7.11.). Определить долю вариации под влиянием условий эксплуатации в общей вариации пробега до капитального ремонта. Сформулировать вывод. Таблица 7.11
7.18. Как повысить точность оценки по уравнению регрессии: а) увеличить объём исходной информации, используемой для расчёта параметров уравнения регрессии; б) использовать более высокий уровень доверительной вероятности (например, P=0, 997 вместо P=0, 95); в) уменьшить уровень доверительной вероятности (например, вероятность 0, 954 вместо вероятности P=0, 997); г) все утверждения неверны. Выберите правильный вариант ответа. 7.19. При производстве керамических изделий была выявлена зависимость уровня брака от влажности используемой массы. Линейный коэффициент корреляции составил 0, 69, корреляционное отношение – 0, 78, общее число наблюдений – 50. При расчёте корреляционного отношения были выделены 4 группы, на которые был разделён раздел диапазон факторного признака. Определить, возможно ли применение линейного уравнения регрессии, если использовать показатель ω 2 при вероятности 0, 95. 7.20. Имеются данные о связи между средней взвешенной ценой и объемом продаж облигаций на ММВБ 23.02.2001 г.:
Составьте линейное уравнение регрессии. Вычислите параметры и рассчитайте линейный коэффициент корреляции. Сформулируйте выводы. 7.21. Зависимость между объемом произведенной продукции и балансовой прибылью по 10 предприятиям одной из отраслей промышленности характеризуется следующими данными:
Определите вид корреляционной зависимости, постройте уравнение регрессии, рассчитайте параметры уравнения, вычислите тесноту связи. Объясните полученные статистические характеристики. 7.22. Имеются следующие данные о посевной площади зерновых культур, валовом сборе и внесении минеральных удобрений на 1 га посевной площади:
Постройте множественное уравнение регрессии, предварительно сформулировав и обосновав выбор результативного и факторных признаков, рассчитайте параметры уравнения, вычислите множественный и частный коэффициенты корреляции. Проанализируйте полученные результаты. 9.23. В ходе проведенного обследования оценки уровня жизни работающих на предприятиях различной формы собственности было опрошено 100 респондентов. Результаты опроса пред ставлены в следующей таблице:
Рассчитайте коэффициенты ассоциации и контингенции. Сформулируйте выводы, вытекающие из анализа полученных коэффициентов. 9.24. Распределение предприятий по источникам средств для их покупки характеризуется следующими данными:
Вычислите коэффициенты ассоциации и контингенции. Какие выводы можно сделать на основании значений этих коэффициентов? 9.25. Зависимость сокращения рабочих от места работы исследовалась в ходе социологического опроса 200 респондентов, результаты которого представлены в следующей таблице:
Определите коэффициенты ассоциации и контингенции. Проанализируйте полученные результаты.
|





 – дисперсия себестоимости по группам предприятий, выделенным по уровню производительности труда;
– дисперсия себестоимости по группам предприятий, выделенным по уровню производительности труда;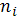 – число предприятий в каждой группе.
– число предприятий в каждой группе.