| Выборочное наблюдение
| вид несплошного наблюдения, который дает возможность судить в целом о всей совокупности (генеральной) на основе обследования только части специально отобранных единиц (выборочной совокупности или выборки)
|
| Условия отбора единиц в выборочную совокупность
| 1. каждая единица генеральной совокупности должна иметь равные возможности попасть в выборку;
2. количество единиц в выборке должно быть достаточно большим
|
| Основные способы формирования выборочной совокупности
|
| Собственно -случайный
| или «метод лото», когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (например, бочонки), которые затем перемешиваются в некоторой емкости (например, в мешке) и выбираются наугад.
На практике применяется жеребьевка или математическая таблица случайных чисел
|
| Повторный отбор
| отобранная из генеральной совокупности единица после её регистрации, возвращается в генеральную совокупность и имеет возможность снова попасть в выборку
|
| Бесповторный отбор
| отобранная единица не возвращается в генеральную совокупность, т.е. не имеет возможности снова попасть в выборку, а оставшиеся единицы имеют большую возможность попасть в выборку, что нарушает первый принцип
|
| Механический
| отбор единиц в выборочную совокупность из генеральной, разбитой по нейтральному признаку на равные интервалы или группы производится таким образом, чтобы из каждой такой группы в выборку попала лишь одна единица
|
| Типологический
| применяется для отбора единиц из неоднородной совокупности. Единицы генеральной совокупности предварительно объединяются по какому-либо типическому признаку в группы, и отбор проводится в пределах этих групп
|
| Серийный
| когда единицы располагаются сериями, отбирать отдельные единицы нецелесообразно, проще организовать отбор серий и провести сплошное обследование выборки
|
| Комбинированный
| представляет собой сочетание перечисленных выше способов отбора. Этот способ более точен
|
| Формулы расчета ошибок выборки
|
| Условные обозначения
| N - численность единиц в генеральной совокупности;
n - численность единиц в выборочной совокупности;
 - средняя величина в генеральной совокупности; - средняя величина в генеральной совокупности;
 - средняя величина в выборочной совокупности;
W - д оля единиц, обладающих признаком в генеральной совокупности
w - доля единиц, обладающих признаком в выборочной совокупности; - средняя величина в выборочной совокупности;
W - д оля единиц, обладающих признаком в генеральной совокупности
w - доля единиц, обладающих признаком в выборочной совокупности;
 - средняя из выборочных дисперсий типических групп; - средняя из выборочных дисперсий типических групп;
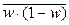 – средняя дисперсия доли признака в выборочной совокупности;
r – число серий в выборочной совокупности;
R – число серий в генеральной совокупности; – средняя дисперсия доли признака в выборочной совокупности;
r – число серий в выборочной совокупности;
R – число серий в генеральной совокупности;
 - межсерийная дисперсия средних; - межсерийная дисперсия средних;
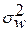 - межсерийная дисперсия доли;
µ - ошибка выборки. - межсерийная дисперсия доли;
µ - ошибка выборки.
|
| При собственно-случайном повторном отборе
|  - для средней; - для средней;
 - для доли - для доли
|
| При случайном и механическом бесповторном отборе
|  - для средней; - для средней;
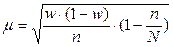 - для доли - для доли
|
| При типологическом бесповторном отборе
| 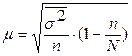 - для средней; - для средней;
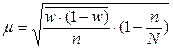 - для доли - для доли
|
| При серийном бесповторном отборе с равновеликими сериями
|  - для средней; - для средней;
 - для доли - для доли
|
Предельная ошибка выборки ( ) )
|  ,
t – нормированное отклонение или «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка (приложение 1) ,
t – нормированное отклонение или «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка (приложение 1)
|
| Интервальная оценка характеристик генеральной совокупности
| для средней:
 или или 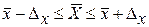 ;
для доли: ;
для доли:
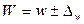 или или 
|
| Формулы определения оптимальной численности выборки
|
| При собственно-случайном повторном отборе
|  - для средней; - для средней;
 - для доли - для доли
|
| При случайном и механическом бесповторном отборе
|  - для средней; - для средней;
 - для доли - для доли
|
| При типологическом бесповторном отборе
|  - для средней; - для средней;
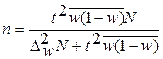 - для доли - для доли
|
| При серийном бесповторном отборе с равновеликими сериями
|  - для средней; - для средней;
 - для доли - для доли
|