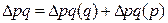1.Ряд динамики – это:
а) множество единиц, обладающих массовостью, однородностью, расположенных в определенном порядке;
б) распределение по варьирующему признаку единиц совокупности;
в) расположенные во временной последовательности числовые значения статистического показателя;
г) нет правильного ответа.
2.Абсолютный прирост исчисляется как:
а) отношение уровней ряда;
б) разность уровней ряда.
3.Имеется следующий ряд динамики:
Производство молока в России, млн. т
|
| 1992г.
| 1993г.
| 1994г.
| 1995г.
| 1996г.
| 1997г.
|
| Млн. т
| 47, 2
| 46, 5
| 44, 2
| 39, 2
| 35, 8
| 34, 1
|
Определить вид ряда динамики:
а) интервальный, полный;
б) интервальный, неполный;
в) моментный, полный;
г) моментный, неполный.
4. Средний темп роста определяется как:
а)  ;
;
б)  *100.
*100.
5.Продажа мяса птицы на рознично-оптовом рынке за январь – май увеличилась в 2, 15 раза. Определить среднемесячный темп роста продажи:
а) 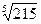 ;
;
б)  ;
;
в)  .
.
6.Коэффициент роста представляет собой:
а) отношение уровней ряда;
б) разность уровней ряда.
7.Абсолютное значение одного процента прироста характеризует:
а) абсолютную скорость роста (снижения) уровней ряда динамики;
б) интенсивность изменения уровней;
в) относительное изменение абсолютного прироста уровня ряда динамики;
г) содержание одного процента прироста в абсолютном выражении.
8. Средний уровень ряда в интервальных полных рядах динамики определяется как:
а)  ;
;
б)  ;
;
в)  .
.
9. Имеется следующий ряд динамики:
Численность коров в России (на 1 января, млн. голов)
|
| 1992г.
| 1993г.
| 1994г.
| 1995г.
| 1996г.
| 1997г.
|
| Млн. голов
| 20, 2
| 19, 8
| 18, 4
| 17, 4
| 15, 8
| 14, 5
|
Определить вид ряда динамики:
а) интервальный, полный;
б) моментный, полный;
в) интервальный, неполный;
г) моментный, неполный.
10.Определение неизвестных промежуточных уровней ряда динамики - это:
а) интерполяция;
б) экстраполяция;
в) корреляция.
11. Ряд динамики, в котором уровни ряда представлены на конкретную дату, называется:
а) полный ряд;
б) конкретный ряд;
в) моментный ряд.
12. Базисный коэффициент роста определяется по формуле:
а)  ;
;
б)  ;
;
в)  .
.
13. Средний уровень в моментных полных рядах динамики определяется как:
а)  ;
;
б)  ;
;
в) 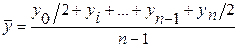 ;
;
г) нет верного ответа.
14. Показатель, определяемый как отношение данного уровня к предыдущему или базисному в процентах, называется:
а) темп прироста;
б ) темп роста;
в) тенденция развития;
г) нет верного ответа.
15. Ряд динамики, характеризующий изменение урожайности сахарной свеклы в фермерском хозяйстве за 10 лет, аналитически можно представить уравнением  . Это значит, что урожайность сахарной свеклы увеличивается ежегодно в среднем на:
. Это значит, что урожайность сахарной свеклы увеличивается ежегодно в среднем на:
а) 13%;
б) 13ц;
в) 1, 3ц.
Тема 8. ИНДЕКСЫ
Индекс – относительный показатель, характеризующий изменение величины простого или сложного явления во времени, пространстве или по сравнению с любым эталоном (план, прогноз, норматив и т.д.).
Основным элементом индексного отношения является индексируемая величина, т.е. величина признака статистической совокупности, изменение которой является объектом изучения. Вторая величина отношения, позволяющая привести разнородные элементы в сопоставимый вид, называется коэффициентом соизмерения или весом индекса.
Основные понятия и показатели индексов
| Индексы количественных показателей
| являются объемными (количественными), поскольку характеризуют общий суммарный размер того или иного явления и выражаются абсолютными величинами. При их расчете объемные показатели оцениваются в сопоставимых ценах
|
| Индексы качественных показателей
| характеризуют уровень явления в расчете на количественно измеримую единицу совокупности: цена за единицу продукции, себестоимость единицы продукции, выработка в единицу времени (или на одного работника), заработная плата одного работника, урожайность с 1 га и т.д.
|
| Индивидуальные индексы
| характеризуют изменение отдельных элементов сложного явления
|
| Индивидуальный индекс цен
| характеризует изменение цен по одному виду продукции и определяется по формуле:
 ,
где p1 - цена за единицу в отчетном периоде,
p0 - цена за единицу в базисном периоде. ,
где p1 - цена за единицу в отчетном периоде,
p0 - цена за единицу в базисном периоде.
|
| Индивидуальный индекс физического объема
|  ,
где q1 - физический объем продукции в отчетном периоде,
q0 - физический объем продукции в базисном периоде ,
где q1 - физический объем продукции в отчетном периоде,
q0 - физический объем продукции в базисном периоде
|
| Индивидуальный индекс себестоимости
|  ,
где z1 - себестоимость единицы в отчетном периоде,
z0 - себестоимость единицы в базисном периоде ,
где z1 - себестоимость единицы в отчетном периоде,
z0 - себестоимость единицы в базисном периоде
|
| Индивидуальный индекс издержек или затрат
| 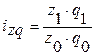 ,
где z1q1 - затраты на производство и реализацию продукции в отчетном периоде,
z0q0 - затраты на производство и реализацию продукции в базисном периоде ,
где z1q1 - затраты на производство и реализацию продукции в отчетном периоде,
z0q0 - затраты на производство и реализацию продукции в базисном периоде
|
| Индивидуальный индекс товарооборота или стоимости
| 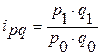 ,
где p1q1 - стоимость продукции (товарооборот) в отчетном периоде,
p0q0 - стоимость продукции (товарооборот) в базисном периоде ,
где p1q1 - стоимость продукции (товарооборот) в отчетном периоде,
p0q0 - стоимость продукции (товарооборот) в базисном периоде
|
| Общий индекс
| характеризует изменение всех элементов сложного явления
|
| Агрегатный индекс стоимости продукции или товарооборота
| показывает, во сколько раз выросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным:
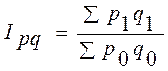
|
| Агрегатный индекс цен Ласпейреса(индекс с весами базисного периода)
| используется для характеристики среднего изменения цен на потребительские товары
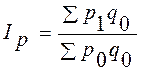 ,
где q0 - потребительская корзина (базовый период);
p0 и p1 - соответственно цены базисного и отчетного периодов ,
где q0 - потребительская корзина (базовый период);
p0 и p1 - соответственно цены базисного и отчетного периодов
|
| Агрегатный индекс цен Паше(индекс с весами отчетного периода)
| если количество набора продуктов принимается на уровне отчетного периода (q1), то в этом случае индекс цен именуется индексом Пааше:

|
| Индекс физического объема
|  , ,

|
| Средний гармонический индекс цен
| 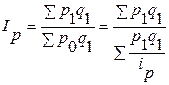
|
| Средний арифметический индекс физического объема
| 
|
| Цепные индексы
| получают путем сопоставления текущих уровней с предшествующим, при этом база сравнения постоянно меняется
|
| Базисные индексы
| получают путем сопоставления с тем уровнем периода, который был принят за базу сравнения
|
| Система индексов с постоянными весами
| это система индексов одного и того же явления, вычисленных с весами, неменяющимися при переходе от одного индекса к другому.
Система базисных индексов с постоянными весами:
 ; ; 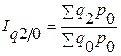 ; ; 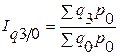 .
Система цепных индексов с постоянными весами: .
Система цепных индексов с постоянными весами:
 ; ;  ; ;  . .
|
| Система индексов с переменными весами
| это система индексов одного и того же явления, вычисленных с весами, последовательно меняющимися при переходе от одного индекса к другому.
Система базисных индексов с переменными весами:
 ; ;  ; ;  .
Система цепных индексов с переменными весами: .
Система цепных индексов с переменными весами:
 ; ;  ; ;  . .
|
| Индекс цен переменного состава
| 
 где
где  - доли каждого товара соответственно в базисном и отчетном периодах. - доли каждого товара соответственно в базисном и отчетном периодах.
|
| Индекс цен постоянного (фиксированного) состава
| 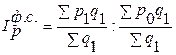 или
или  . .
|
| Индекс цен структурных сдвигов
|  или
или 
|
| Взаимосвязь индексов
| 
|
| Индексы физического объема и цен
| являются факторными по отношению к индексу стоимости продукции:
 ; ;
 Разложение абсолютного прироста стоимости продукции по факторам можно записать в виде:
Разложение абсолютного прироста стоимости продукции по факторам можно записать в виде:
 - абсолютный прирост (уменьшение) товарооборота за счет изменения цен и физического объема в отчетном периоде по сравнению с базисным; - абсолютный прирост (уменьшение) товарооборота за счет изменения цен и физического объема в отчетном периоде по сравнению с базисным;
 - абсолютный прирост (уменьшение) товарооборота за счет изменения физического объема; - абсолютный прирост (уменьшение) товарооборота за счет изменения физического объема;
 - абсолютное изменение товарооборота за счет изменения цен в отчетном периоде по сравнению с базисным.
Взаимосвязь: - абсолютное изменение товарооборота за счет изменения цен в отчетном периоде по сравнению с базисным.
Взаимосвязь: 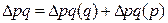
|

 ;
; *100.
*100.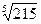 ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
.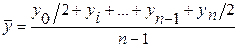 ;
; . Это значит, что урожайность сахарной свеклы увеличивается ежегодно в среднем на:
. Это значит, что урожайность сахарной свеклы увеличивается ежегодно в среднем на: ,
где p1 - цена за единицу в отчетном периоде,
p0 - цена за единицу в базисном периоде.
,
где p1 - цена за единицу в отчетном периоде,
p0 - цена за единицу в базисном периоде.
 ,
где q1 - физический объем продукции в отчетном периоде,
q0 - физический объем продукции в базисном периоде
,
где q1 - физический объем продукции в отчетном периоде,
q0 - физический объем продукции в базисном периоде
 ,
где z1 - себестоимость единицы в отчетном периоде,
z0 - себестоимость единицы в базисном периоде
,
где z1 - себестоимость единицы в отчетном периоде,
z0 - себестоимость единицы в базисном периоде
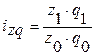 ,
где z1q1 - затраты на производство и реализацию продукции в отчетном периоде,
z0q0 - затраты на производство и реализацию продукции в базисном периоде
,
где z1q1 - затраты на производство и реализацию продукции в отчетном периоде,
z0q0 - затраты на производство и реализацию продукции в базисном периоде
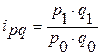 ,
где p1q1 - стоимость продукции (товарооборот) в отчетном периоде,
p0q0 - стоимость продукции (товарооборот) в базисном периоде
,
где p1q1 - стоимость продукции (товарооборот) в отчетном периоде,
p0q0 - стоимость продукции (товарооборот) в базисном периоде
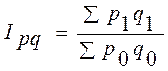
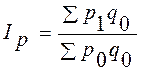 ,
где q0 - потребительская корзина (базовый период);
p0 и p1 - соответственно цены базисного и отчетного периодов
,
где q0 - потребительская корзина (базовый период);
p0 и p1 - соответственно цены базисного и отчетного периодов

 ,
,

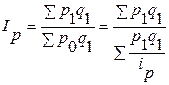

 ;
; 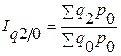 ;
; 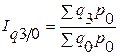 .
Система цепных индексов с постоянными весами:
.
Система цепных индексов с постоянными весами:
 ;
;  .
.
 ;
;  ;
;  .
Система цепных индексов с переменными весами:
.
Система цепных индексов с переменными весами:
 ;
;  .
.

 где
где  - доли каждого товара соответственно в базисном и отчетном периодах.
- доли каждого товара соответственно в базисном и отчетном периодах.
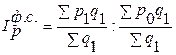 или
или  .
.
 или
или 

 ;
;
 Разложение абсолютного прироста стоимости продукции по факторам можно записать в виде:
Разложение абсолютного прироста стоимости продукции по факторам можно записать в виде:
 - абсолютный прирост (уменьшение) товарооборота за счет изменения цен и физического объема в отчетном периоде по сравнению с базисным;
- абсолютный прирост (уменьшение) товарооборота за счет изменения цен и физического объема в отчетном периоде по сравнению с базисным;
 - абсолютный прирост (уменьшение) товарооборота за счет изменения физического объема;
- абсолютный прирост (уменьшение) товарооборота за счет изменения физического объема;
 - абсолютное изменение товарооборота за счет изменения цен в отчетном периоде по сравнению с базисным.
Взаимосвязь:
- абсолютное изменение товарооборота за счет изменения цен в отчетном периоде по сравнению с базисным.
Взаимосвязь: