| Средняя величина
| отражает типичный уровень признака и абстрагируется от индивидуальных особенностей, присущих отдельным единицам
|
| Классы средних величин
| 1) с тепенные средние:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая и др.
2) структурные средние:
- мода;
- медиана;
- квартили;
- перцентили;
- децили и др.
|
| Средние степенные величины
|
| Степенная
| простая средняя:
 ;
взвешенная средняя: ;
взвешенная средняя:
 где
где 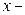 варианты признака; варианты признака;
 среднее значение признака; среднее значение признака;
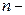 число вариантов признака, число вариантов признака,  ; ;
 частоты; частоты;
 показатель степени показатель степени
|
Гармоническая

| простая средняя:
 ;
взвешенная средняя: ;
взвешенная средняя:
 , где , где 
|
Геометрическая
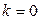
| простая средняя:
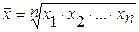 ;
взвешенная средняя: ;
взвешенная средняя:

|
Арифметическая 
| простая средняя:
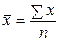 ;
взвешенная средняя: ;
взвешенная средняя:

|
Квадратическая

| простая средняя:
 ;
взвешенная средняя: ;
взвешенная средняя:
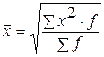
|
| Правило мажорантности средних
| чем больше k в формуле средней степенной, тем больше значение средней величины:

|
| Структурные средние (показатели центра распределения)
|
| Мода (Мо)
| представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой:
 ,
где ,
где  – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
 – длина модального интервала; – длина модального интервала;
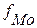 – частота модального интервала; – частота модального интервала;
 – частота интервала, предшествующего модальному; – частота интервала, предшествующего модальному;
 – частота интервала, следующего за модальным – частота интервала, следующего за модальным
|
| Медиана (Ме)
| значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности:
 ,
где ,
где  – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого равна или превышает половину общей суммы частот); – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого равна или превышает половину общей суммы частот);
 – длина медианного интервала; – длина медианного интервала;
 – частота медианного интервала; – частота медианного интервала;
 – накопленная частота интервала, предшествующего медианному – накопленная частота интервала, предшествующего медианному
|
| Квартиль
| значения признака, делящие ранжированную совокупность на 4 равные части:
 , , 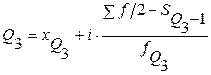 ,
где ,
где  - нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%); - нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
 - нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%); - нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
 - длина интервала; - длина интервала;
 - накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль; - накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
 - накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль; - накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;
 - частота интервала, содержащего нижний квартиль; - частота интервала, содержащего нижний квартиль;
 - частота интервала, содержащего верхний квартиль - частота интервала, содержащего верхний квартиль
|
| Дециль
| характеризует распределение величин совокупности, при которой девять значений дециля делят ее на десять равных частей. Любая из этих десяти частей составляет 1/10 всей совокупности. Так, первый дециль отделяет 10 % наименьших величин, лежащих ниже дециля от 90 % наибольших величин, лежащих выше дециля:
 , , 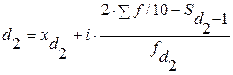 и т.д. и т.д.
|
| Коэффициент децильной дифференциации
| показывает, во сколько раз наименьший уровень признака из 10% единиц, имеющих наибольший уровень признака, больше наибольшего уровня признака из 10% единиц совокупности, имеющих наименьший уровень признака. Применяется для характеристики дифференциации населения по уровню дохода:

|
| Коэффициент фондовой дифференциации
| отражает масштабы расслоения населения (отношение среднего дохода 10% самых богатых жителей страны к среднему доходу 10% беднейших):
 ,
где ,
где  - средний уровень признака из 10% наибольших значений признака; - средний уровень признака из 10% наибольших значений признака;
 - средний уровень признака из 10% наименьших значений признака - средний уровень признака из 10% наименьших значений признака
|
| Показатели вариации
|
| Вариация
| различия в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период, момент времени
|
| Показатели вариации
| отклонения индивидуальных значений признака от их среднего значения. Чем меньше эти отклонения, тем средняя более показательна, надежна
|
| Размах вариации
| показывает разность между наибольшим ( ) и наименьшим ( ) и наименьшим ( ) значениями варьирующего признака: ) значениями варьирующего признака:

|
| Среднее линейное отклонение
| средняя арифметическая из абсолютных значений отклонений вариантов признака от их среднего значения  : :
 - простое среднее линейное отклонение; - простое среднее линейное отклонение;
 - взвешенное среднее линейное отклонение. - взвешенное среднее линейное отклонение.
|
| Дисперсия
| представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины:
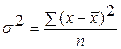 простая дисперсия; простая дисперсия;
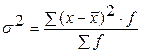 взвешенная дисперсия взвешенная дисперсия
|
| Среднее квадратическое отклонение
| Представляет собой корень квадратной из дисперсии:
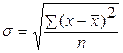 простое среднее квадратическое отклонение; простое среднее квадратическое отклонение;
 взвешенное среднее квадратическое отклонение взвешенное среднее квадратическое отклонение
|
| Коэффициент вариации
| относительная мера колеблемости признака:
 .
Если .
Если  < 33 %, то вариация признака считается незначительной, а совокупность единиц, обладающих этим признаком - однородной < 33 %, то вариация признака считается незначительной, а совокупность единиц, обладающих этим признаком - однородной
|
| Дисперсионный анализ
|
| Общая дисперсия (σ 2общ)
| измеряет вариацию признака по всей совокупности под влиянием всех факторов, ее обусловивших. Она равна среднему квадрату отклонений отдельных значений признака х от общей по совокупности средней  и может быть вычислена как простая дисперсия или взвешенная дисперсия и может быть вычислена как простая дисперсия или взвешенная дисперсия
|
| Межгрупповая дисперсия (σ 2межгр)
| характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних  от общей средней от общей средней  :
σ 2межгр = :
σ 2межгр =  ,
где f — численность единиц в группе ,
где f — численность единиц в группе
|
| Внутригрупповая (частная) дисперсия (σ 2i)
| отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака х внутри группы от средней арифметической этой группы  (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
σ 2 i = (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
σ 2 i =  ;
σ 2 i = ;
σ 2 i =  .
На основании внутригрупповой дисперсии по каждой группе (σ 2 i) можно определить общую среднюю из внутригрупповых дисперсий: .
На основании внутригрупповой дисперсии по каждой группе (σ 2 i) можно определить общую среднюю из внутригрупповых дисперсий:
 = = 
|
| Правило сложения дисперсий
| σ 2общ = σ 2межгр + 
|
| Эмпирический коэффициент детерминации (η 2)
| представляет собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризует силу влияния группировочного признака на образование общей вариации:
η 2 =  . .
|
| Эмпирическое корреляционное отношение
| показывает тесноту связи между группировочным и результативным признаками:
η =  . .
|