Тесты для самоконтроля. 1. Выработка 7 членов бригады характеризуется следующими данными (деталей за смену): 18, 26, 27, 21
1. Выработка 7 членов бригады характеризуется следующими данными (деталей за смену): 18, 26, 27, 21, 21, 24, 28. Определить медианное значение: а) 21; б) 24; в) 23, 5.
2.По предприятию известны следующие данные:
Какую формулу средней следует использовать для расчета средней заработной платы по предприятию в целом? а) среднюю арифметическую простую; б) среднюю арифметическую взвешенную; в) среднюю геометрическую; г) среднюю гармоническую взвешенную.
3.Какой из показателей вариации характеризует относительную меру колеблемости статистического признака около средней величины: а) коэффициент вариации; б) дисперсия; в) среднее квадратическое отклонение; г) нет правильного ответа.
4. Могут ли мода, медиана и средняя арифметическая совпадать: а) могут; б) могут совпадать только средняя и медиана; в) не могут.
5.Средний уровень моментного ряда с равными промежутками между датами вычисляется по формуле: а) средней арифметической простой; б) средней хронологической простой; в) средней арифметической взвешенной; г) нет правильного ответа.
6.Распределение торговых предприятий города по числу работников характеризуется следующими данными:
Определить модальный интервал: а) 4 - 10; б) 11 - 20; в) 21 - 40.
7.Дисперсия – это: а) средняя арифметическая абсолютных отклонений вариантов от их среднего значения; б) разность между максимальным и минимальным значением признака; в) средний квадрат отклонений вариантов от их средней величины; г) нет правильного ответа.
8. Если дисперсия признака в совокупности А больше дисперсии признака в совокупности Б, то: а) коэффициент вариации в совокупности А будет меньше; б) коэффициент вариации в совокупности А также будет больше; в) коэффициент вариации в совокупности А может быть как больше, так и меньше.
9.Среднюю арифметическую простую используют в следующем случае: а) находится средняя из средних; б) осредняемый признак – количественный; в) осредняемый признак – качественный; г) нет правильного ответа.
10.По какому графическому изображению ряда распределения определяют медиану: а) гистограмма; б) полигон; в) кумулята.
11.Упрощенная формула дисперсии выглядит следующим образом: а) б) в)
12. Различают следующие классы средних величин: а) вариационные и степенные; б) вариационные и структурные; в) структурные и степенные; г) простые и взвешенные.
13.Имеются следующие данные:
Какой вид степенной средней необходимо использовать для нахождения среднего темпа роста: а) среднюю арифметическую простую; б) среднюю геометрическую взвешенную; в) среднюю геометрическую простую; г) среднюю гармоническую.
14. Как изменится дисперсия признака, если все варианты признака увеличить в 3 раза: а) возрастет в 3 раза; б) увеличится в 9 раз; в) не изменится.
15. Как изменится средняя величина, если все варианты признака уменьшить в 1, 5 раза, а все веса увеличить в 1, 5 раза: а) не изменится; б) уменьшится; в) увеличится.
16.Распределение торговых предприятий города по числу работников характеризуется следующими данными:
Определить медианный интервал: а) 4 - 10; б) 11 - 20; в) 21 - 40.
Тема 7. РЯДЫ ДИНАМИКИ Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (РД). Ряд динамики (или временной ряд)–это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке). Составными элементами ряда динамики являются показатели – уровни ряда и периоды или моменты времени. Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Моменты (даты) или периоды времени, к которым относятся уровни, обозначают через t. С помощью рядов динамики изучение закономерностей развития социально-экономических явлений осуществляется в следующих направлениях: - характеристика уровней развития изучаемых явлений во времени; - измерение динамики изучаемых явлений посредством системы статистических показателей; - выявление и количественная оценка основной тенденции развития (тренда); - изучение периодических колебаний; - экстраполяция и прогнозирование. Виды РД: · по способу выражения уровней ряда различают ряды: - абсолютных величин; - относительных величин; - средних величин. · по времени, отражаемому в динамических рядах: - моментные (ряды, уровни которых характеризуют размер признака на определенную дату, например, на начало месяца); - интервальные (периодные) (ряды, уровни которых характеризуют размер признака за период времени, например, за квартал, за год и т.д.). · в зависимости от расстояния между уровнями: - полные – ряды динамики, в которых даты следуют друг за другом через равные промежутки времени или интервалы времени, на которые заданы уровни, равны; - неполные, когда периоды времени между датами неодинаковые или равенство интервалов времени не соблюдается. Основные понятия и показатели рядов динамики
|

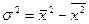 ;
;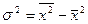 ;
; .
. - базисный абсолютный прирост;
- базисный абсолютный прирост;
 - цепной абсолютный прирост.
где
- цепной абсолютный прирост.
где 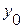 – начальный уровень (базисный);
– начальный уровень (базисный);
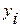 – какой-либо уровень;
– какой-либо уровень;
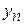 – конечный уровень.
Взаимосвязь: сумма всех последовательных цепных абсолютных приростов равна базисному абсолютному приросту за исследуемый период (последнему базисному):
– конечный уровень.
Взаимосвязь: сумма всех последовательных цепных абсолютных приростов равна базисному абсолютному приросту за исследуемый период (последнему базисному):
 .
.
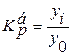 .
Коэффициент роста цепной:
.
Коэффициент роста цепной:
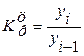 .
Темп роста:
Тр=К ·100%.
.
Темп роста:
Тр=К ·100%.
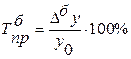 - базисный темп прироста;
- базисный темп прироста;
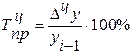 - цепной темп прироста.
Он может быть вычислен и по такой формуле:
- цепной темп прироста.
Он может быть вычислен и по такой формуле:
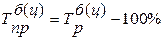
 .
Абсолютное значение одного процента прироста может быть вычислено и по такой формуле:
.
Абсолютное значение одного процента прироста может быть вычислено и по такой формуле:
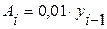
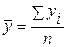 (формула средней арифметической простой);
· с неравными интервалами:
(формула средней арифметической простой);
· с неравными интервалами:
 (формула средней арифметической взвешенной),
где t – периоды времени.
Б) в моментных рядах:
· с равноотстоящими уровнями:
(формула средней арифметической взвешенной),
где t – периоды времени.
Б) в моментных рядах:
· с равноотстоящими уровнями:
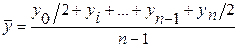 (формула средней хронологической),
где
(формула средней хронологической),
где 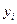 – уровни ряда,
n – число уровней.
· с неравноотстоящими уровнями:
– уровни ряда,
n – число уровней.
· с неравноотстоящими уровнями:
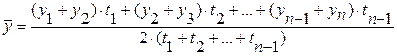 ,
где n- 1- число промежутков времени между уровнями
,
где n- 1- число промежутков времени между уровнями
 ,
где n – 1– число цепных абсолютных приростов.
С использованием взаимосвязи цепных и базисных абсолютных приростов:
,
где n – 1– число цепных абсолютных приростов.
С использованием взаимосвязи цепных и базисных абсолютных приростов:
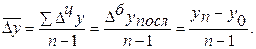
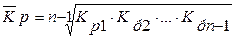 (формула средней геометрической),
где Кр1 , Кр2,..., Кр n-1 - коэффициенты роста по сравнению с предыдущим периодом;
n - число уровней ряда.
Используя взаимосвязь цепных и базисных темпов роста, получают следующую формулу для вычисления среднего коэффициента роста:
(формула средней геометрической),
где Кр1 , Кр2,..., Кр n-1 - коэффициенты роста по сравнению с предыдущим периодом;
n - число уровней ряда.
Используя взаимосвязь цепных и базисных темпов роста, получают следующую формулу для вычисления среднего коэффициента роста:
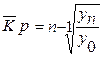
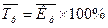
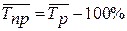
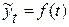 ,
где
,
где 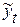 - уровни РД, вычисленные по аналитическому уравнению на момент времени t.
Простейшими моделями являются:
линейная функция:
- уровни РД, вычисленные по аналитическому уравнению на момент времени t.
Простейшими моделями являются:
линейная функция: 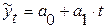 ,
где
,
где 
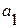 - параметры уравнения;
t – порядковый номер периода.
парабола:
- параметры уравнения;
t – порядковый номер периода.
парабола: 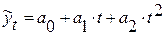 ,
экспонента:
,
экспонента: 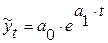
 ,
где
,
где  - коэффициент доверия, который определяется по таблице t –распределения Стьюдента при уровне значимости
- коэффициент доверия, который определяется по таблице t –распределения Стьюдента при уровне значимости  (т.е. с вероятностью P=0, 95) и числе степеней свободы
(т.е. с вероятностью P=0, 95) и числе степеней свободы 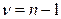 (приложение 1)
(приложение 1)
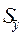 - средняя квадратическая ошибка средней величины:
- средняя квадратическая ошибка средней величины: 
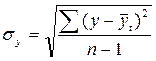 - остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы (n – m),
где n – число уровней РД.
2) по среднему абсолютному приросту:
- остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы (n – m),
где n – число уровней РД.
2) по среднему абсолютному приросту:
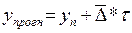 ,
где уn – последний известный уровень РД;
τ – период упреждения (срок прогнозирования).
Данный метод используется для краткосрочного прогнозирования.
3) по среднему коэффициенту роста:
,
где уn – последний известный уровень РД;
τ – период упреждения (срок прогнозирования).
Данный метод используется для краткосрочного прогнозирования.
3) по среднему коэффициенту роста:
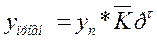 Данный метод может использоваться и в краткосрочном и в долгосрочном прогнозировании.
Данный метод может использоваться и в краткосрочном и в долгосрочном прогнозировании.



