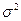Решение типовых задач. №1. Имеются следующие данные о производительности труда рабочих в двух бригадах:
№1. Имеются следующие данные о производительности труда рабочих в двух бригадах: Таблица №3.1
Определить: 1) размах вариации 3) среднее квадратичное отклонение Решение: 1. 2. Для первичного ряда среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчета среднего линейного отклонения следующий: а) по значениям признака исчисляется средняя арифметическая: б) определяются отклонения каждой варианты Х от средней: в) рассчитывается сумма абсолютных величин отклонений: г) сумма абсолютных величин отклонений делится на число значений:
В нашем примере средняя производительность труда рабочих первой бригады-
- второй бригады
Таблица 3.2
Считается, что среднее линейное отклонение дает необъективную оценку вариации, как правило, занижает ее. 3. Корень квадратный из дисперсии называется средним квадратическим отклонением
Для первой бригады:
Для второй бригады:
Среднеквадратическое отклонение является наиболее распространенным показателем степени вариации. 4. Коэффициент вариации – относительный показатель колеблемости, равный процентному отношению среднего квадратического отклонения к средней арифметической:
Для первой бригады:
Для второй бригады:
Анализ полученных данных говорит о том, что производительность труда работников первой бригады отличается от средней производительности труда ( №2. При изучении норм расхода сырья получили следующее распределение изделий по весу:
Вычислите: 1) среднее линейное отклонение; 2) среднее квадратическое отклонение; 3) коэффициент вариации. Решение: 1. В вариационном ряду среднее линейное отклонение определяется по формуле:
Расчет этой величины удобно осуществлять в таблице.
Следовательно, вес изделий отклоняется от среднеарифметического веса в среднем на 1, 285 г. 2. Среднее квадратическое отклонение вариационного интервального ряда определяется по формуле:
Предоставив необходимые расчеты в таблице, подсчитаем:
3. Коэффициент вариации:
Так как V< 40%, то средний вес изделий, равный 22, 7 г., является типичной величиной в данной однородной совокупности, и вес изделий от среднего веса в среднем отклоняется на 1, 9 или на 8, 48%.
№ 3. Имеется статистическая информация о фондоотдаче тридцати организаций, руб.: 1, 05; 0, 96; 1, 12; 1, 19; 1, 08; 1, 98; 1, 3; 1, 16; 1, 065; 1, 0; 1, 1; 1, 23; 1, 13; 1, 03; 0, 9; 1, 06; 1, 15; 1, 07; 1, 17; 0, 94; 1, 02; 1, 06; 1, 18; 0, 99; 1, 1; 1, 28; 1, 09; 1, 25; 1, 04; 1, 12.
1. Постройте статистический ряд распределения организаций по фондоотдаче, образовав пять групп с равными интервалами. 2. Постройте графики полученного ряда распределения. Графически определите значения моды и медианы. 3. Рассчитайте характеристики ряда распределения: среднюю арифметическую, моду и медиану, квадратическое отклонение, коэффициент вариации. 4. Вычислите среднюю арифметическую по исходным данным, сравните ее с аналогичным показателем, рассчитанным в п. 3. Объясните причину их расхождения. Решение: Необходимо построить ряд распределения организаций по признаку «фондоотдача», образовав пять групп с равными интервалами. Величину интервала группировки организаций по фондоотдаче определяем по формуле:
Таким образом, интервалы получились: 0, 9 – 0, 98; 0, 98 – 1, 06; 1, 06 – 1, 14; 1, 14 – 1, 22; 1, 22 – 1, 3. Подсчитаем частоты, частости и накопленные частоты и представим результаты в таблице 3.3: Таблица 3.3 Ряд распределения организаций по фондоотдаче
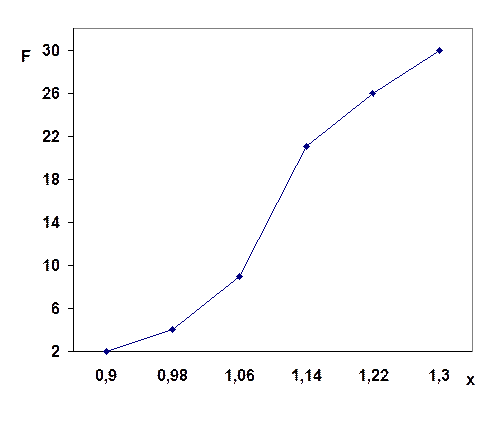
2. Ряды распределения могут быть изображены графически. Основные графики следующие: - полигон частот ряда распределения организаций по фондоотдаче (рис. 3. 1); - гистограмма ряда распределения организаций по фондоотдаче (рис.3.2); - кумулята распределения организаций по фондоотдаче (рис. 3.3).
Рис.3.1 Полигон частот ряда распределения организаций по фондоотдаче
1.092 0.9 0, 98 1, 06 1, 14 1, 22 1, 3
Рис.3. 2 Гистограмма ряда распределения организаций по фондоотдаче
1, 096
Рис. 3.3 Кумулята ряда распределения организаций по фондоотдаче
Анализ ряда и графиков показывает, что распределение организаций по фондоотдаче не является равномерным, чем больше фондоотдача организаций отличается от средней фондоотдачи, тем реже такие организации встречаются. 3. Чтобы найти моду, первоначально определим модальный интервал данного ряда. Из таблицы 3.3 видно, что наибольшая частота соответствует интервалу, где значение варианты лежит в пределах от 1, 06 до 1, 14. Это и есть модальный интервал. Для расчета определенного значения модальной величины признака, заключенного в этом интервале, применяют такую формулу:
где х0 – нижняя граница модального интервала, в нашем случае 1, 06; i - величина интервала группировки, в нашем примере 0, 08; f1 - частота интервала, предшествующему модальному (7); f2 - частота модального интервала (11); f3 - частота интервала следующего за модальным (5). Подставляя числовые значения из нашего задания в эту формулу, получим:
Исчислим теперь медиану. Для нахождения медианы в интервальном вариационном ряде определим сначала интервал, в котором она находится (медианный интервал). Половина суммы частот у нас равна 15. Следовательно, согласно табл. 3.3 медианным интервалом у нас будет интервал со значением фондоотдачи от 1, 06 до 1, 14. Формула для исчисления медианы в вариационном интервальном ряде будет иметь такой вид:
где х0 – нижняя граница медианного интервала; NМе – номер медианы; FМе-1 – накопленная частота интервала, предшествующего медианному; fМе – частота медианного интервала. Подставляя в эту формулу значения, получим:
Средняя арифметическая для ряда распределения определяется по формуле средней арифметической взвешенной (
Следовательно, средняя арифметическая равна 1, 1; мода-1, 092 и медиана- 1, 096. Соотношение этих трех величин указывает на направление и степень асимметрии распределения. Так как значение средней арифметической больше значения медианы и моды, то есть 1, 1 > 1, 096> 1, 092, то это правосторонняя асимметрия (положительная). Правосторонняя асимметрия свидетельствует о прогрессивном развитии отрасли, о том, что оно идет в сторону увеличения эффективности использования основных производственных фондов (увеличения фондоотдачи) организаций. Чтобы вычислить среднее квадратическое отклонение, нужно определить дисперсию признака. Формула этого показателя такая:
Корень квадратный из дисперсии и будет средним квадратическим отклонением:
Проделаем в таблице 3.4 необходимые расчеты для нахождения дисперсии, среднего квадратического отклонения и коэффициента вариации. Таблица 3.4 Вычисление дисперсии, среднего квадратического отклонения и коэффициента вариации
Анализ полученных данных говорит о том, что фондоотдача организаций отличается от средней фондоотдачи на 0, 94 руб., или на 8, 55%. Значение коэффициента вариации v не превышает 40 %. Отсюда следует, что вариация фондоотдачи не высокая и средняя фондоотдача, рассчитанная по средней арифметической взвешенной, является типичной, надежной величиной, свидетельствующей об однородности совокупности. 4. Вычислим среднюю арифметическую по исходным данным и сравним ее с аналогичным показателем, рассчитанным по таблице 3.4. Средняя арифметическая
Данный результат, полученный на основе средней арифметической простой, отличается от средней арифметической взвешенной. Это объясняется тем, что в расчете на основе ряда распределения мы уже не располагаем исходными индивидуальными данными, а вынуждены ограничиваться сведениями о величине середины интервала.
№ 4. Имеются данные о производительности труда рабочих:
Определите: 1) частные дисперсии; 2) среднюю из частных дисперсий; 3) межгрупповую дисперсию; 4) общую дисперсию (по правилу сложения дисперсий и обычным способом); 5) эмпирическое корреляционное отношение. Сделайте выводы. Решение: Это первичные данные. 1. Для расчета групповых дисперсий воспользуемся формулой:
Расчет дисперсий по группам представим в таблице 3.5: Таблица 3.5
Подставив полученные значения в формулу, получим:
2. Средняя из групповых дисперсий равна:
3. Для определения межгрупповой дисперсии предварительно следует подсчитать общую среднюю как среднюю взвешенную из групповых средних:
Затем рассчитаем межгрупповую дисперсию:
4. Общую дисперсию исчислим по правилу сложения дисперсий:
Проверим полученный результат, исчислив общую дисперсию обычным способом:
4) Коэффициент детерминации равен:
Эмпирическое корреляционное отношение составит:
Коэффициент детерминации показывает, какая доля всей вариации признака обусловлена фактором, положенным в основу группировки. Коэффициент детерминации Если связь отсутствует, то корреляционное отношение равно нулю. В этом случае дисперсия групповых средних Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии ( Для качественной оценки тесноты связи на основе показателя
Убедившись с помощью группировки и В нашем примере №4 По исходным данным таблицы 3.6 Таблица 3.6 Статистическая информация о фондоотдаче тридцати организаций
1) установите наличие и характер связи между признаками – выпуском продукции и эффективностью использования основных производственных фондов (фондоотдачей), образовав, пять групп с равными интервалами по обоим признакам, методом аналитической группировки; 2) измерьте тесноту корреляционной связи между названными признаками с помощью использования коэффициента детерминации и эмпирического корреляционного отношения. Сделайте выводы. Решение: 1. Связь между признаками «выпуск продукции» и «фондоотдача» изучается с помощью аналитической группировки. Поскольку аналитическая группировка предполагает разделение совокупности на группы по факторному признаку, его необходимо определить. В нашем примере факторным признаком является фондоотдача, т.к. от нее зависит выпуск продукции. Определяем величину интервала группировки по факторному признаку по формуле:
Группы будут: 0, 9 – 0, 98; 0, 98 – 1, 06; 1, 06 – 1, 14; 1, 14 – 1, 22; 1, 22 – 1, 3. Чтобы дополнить эти данные средними по группам значениями выпуска продукции, необходимо построить рабочую таблицу 3.7: Таблица 3.7 Распределение организаций по фондоотдаче
На основании таблицы 3.7 построим итоговую таблицу 3.8 аналитической группировки. Таблица 3.8 Зависимость выпуска продукции организаций от фондоотдачи
Групповые средние результативного признака определяются по формуле простой средней арифметической:
Общая средняя результативного признака по совокупности в целом может быть определена двумя способами: 1) по первичным данным по формуле простой средней арифметической:
2) по вторичным данным, по формуле взвешенной средней арифметической:
Анализ таблицы 3.8 (графы А и 3) показывает, что с ростом фондоотдачи от группы к группе возрастает и выпуск продукции в среднем на одну организацию. Отсюда следует, что между фондоотдачей и выпуском продукции в среднем на одну организацию существует прямая корреляционная взаимосвязь. 2. Коэффициент детерминации равен Если учесть, что величина межгрупповой дисперсии характеризует влияние только факторного признака, а величина общей дисперсии характеризует влияние всех признаков, влияющих на результативную величину, то частное от деления межгрупповой дисперсии на общую дисперсию укажет на силу влияния факторного признака на результативный. Эмпирическое корреляционное отношение определяется по формуле:
Все расчеты проделаем в таблице 3.9.
Таблица 3.9 Рабочая таблица для определения межгрупповой дисперсии
Межгрупповая дисперсия выпуска продукции равна:
Рассчитаем теперь общую дисперсию уровней выпуска продукции по индивидуальным данным 30 организаций. Для этого составим таблицу 3.10. Опираясь на данные таблицы 3.10, рассчитаем общую дисперсию:
100 – 93, 3 = 6, 8 %. Таблица 3.10 Рабочая таблица для расчета общей дисперсии
Продолжение таблицы 3.10
Выводы: Величина коэффициента детерминации говорит о том, что вариация выпуска продукции на 93, 3 % зависит от вариации фондоотдачи организаций и на 6, 8 % от вариации прочих признаков. Эмпирическое корреляционное отношение, равное 0, 966, свидетельствует о весьма тесной связи между фондоотдачей и выпуском продукции.
Задачи №3.1 В результате обследования работы станков в механических цехах завода получены следующие данные:
Определите: среднее линейное отклонение, среднее квадратическое отклонение, коэффициент вариации времени работы: 1) токарных станков; 2) заточных станков.
№3.2 Имеются следующие данные о количестве произведенной рабочими цеха за смену продукции (в штуках): 10 14 12 15 11 16 14 19 23 13 19 16 19 15 25 21 22
1. Постройте ряд распределения рабочих по количеству произведенной продукции, образовав три группы с равными интервалами. Изобразите ряд графически. 2. По данным ряда распределения определите: а) среднюю выработку продукции (количество произведенной продукции на одного рабочего); б) коэффициент вариации выработки продукции.
№3.3 Имеются следующие данные о распределении рабочих по стажу:
Вычислите: 1. Средний стаж рабочих и среднее квадратическое отклонение. 2. Коэффициент вариации. Поясните полученные результаты. № 3.4 Доля бракованной продукции по пяти цехам завода составила:
По каждому цеху определить дисперсию и среднее квадратическое отклонение доли бракованной продукции.
№3.5 Имеются следующие данные, полученные в результате группировки.
Общая дисперсия результативного признака равна 1, 4. Определите эмпирическое корреляционное отношение.
№3.6 Имеются следующие данные, полученные в результате обследования рабочих цеха.
Определите: общую, межгрупповую и среднюю их групповых дисперсий, коэффициент детерминации, эмпирическое корреляционное отношение. Сделайте выводы.
|

 , 2) среднее линейное отклонение
, 2) среднее линейное отклонение 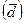 ,
, , 4) коэффициент вариации
, 4) коэффициент вариации  .
. , где
, где  - максимальное значение признака,
- максимальное значение признака, 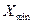 - минимальное значение признака. Для нашего примера размах вариации производительности труда для первой бригады составляет:
- минимальное значение признака. Для нашего примера размах вариации производительности труда для первой бригады составляет: 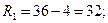 для второй бригады:
для второй бригады: 
 . Этот показатель прост в вычислении и указывает на общие размеры вариации, но он не дает представления о степени колеблемости внутри совокупности, так как вычисляется на основе только двух крайних значений признака совокупности.
. Этот показатель прост в вычислении и указывает на общие размеры вариации, но он не дает представления о степени колеблемости внутри совокупности, так как вычисляется на основе только двух крайних значений признака совокупности. .
. ;
; ;
; ;
; .
. шт.,
шт.,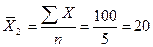 шт.
шт.

 шт.,
шт.,  шт.,
шт., .
. .
. шт.
шт.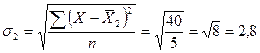 шт.
шт. .
.

 = 20шт.) в среднем на 12, 8 шт., или на 64%, а второй бригады – в среднем на 2, 8 шт., или на 14%. Величины показателей вариации свидетельствуют о том, что совокупность рабочих второй бригады по уровню производительности труда однороднее совокупности рабочих первой бригады. Значение коэффициента вариации рабочих первой бригады превышает 40%, следовательно, вариация производительности труда рабочих велика, найденная средняя производительность труда плохо представляет всю совокупность рабочих, не является ее типичной, надежной характеристикой, а саму совокупность нет оснований считать однородной по производительности труда. Значение коэффициента вариации у рабочих второй бригады не превышает 40 %. Это говорит об относительно невысокой колеблемости признака, о типичности, надежности средней производительности труда, об однородности рабочих второй бригады по производительности труда.
= 20шт.) в среднем на 12, 8 шт., или на 64%, а второй бригады – в среднем на 2, 8 шт., или на 14%. Величины показателей вариации свидетельствуют о том, что совокупность рабочих второй бригады по уровню производительности труда однороднее совокупности рабочих первой бригады. Значение коэффициента вариации рабочих первой бригады превышает 40%, следовательно, вариация производительности труда рабочих велика, найденная средняя производительность труда плохо представляет всю совокупность рабочих, не является ее типичной, надежной характеристикой, а саму совокупность нет оснований считать однородной по производительности труда. Значение коэффициента вариации у рабочих второй бригады не превышает 40 %. Это говорит об относительно невысокой колеблемости признака, о типичности, надежности средней производительности труда, об однородности рабочих второй бригады по производительности труда. , где
, где  .
.
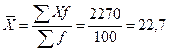 г.
г.  г.
г. .
.
 г.
г.

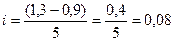 руб.
руб.











 15
15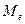
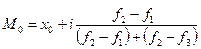 .
. руб.
руб.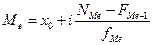 ,
, руб.
руб. см. табл. 3.4, гр.3):
см. табл. 3.4, гр.3):
 руб.
руб.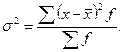



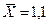 руб.
руб.



 руб.
руб. , где
, где  .
.


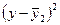
 шт.
шт.  шт.
шт.

 .
. шт.
шт.


 или 15, 2 %.
или 15, 2 %. ;
; 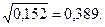
 = 15, 2%, следовательно, фактор времени работы (ночное или дневное) на 15, 2 % обуславливает вариацию производительности труда рабочих. Эмпирическое корреляционное отношение показывает тесноту связи между группировочным и результативным признаками. Корреляционное отношение изменяется от 0 до 1.
= 15, 2%, следовательно, фактор времени работы (ночное или дневное) на 15, 2 % обуславливает вариацию производительности труда рабочих. Эмпирическое корреляционное отношение показывает тесноту связи между группировочным и результативным признаками. Корреляционное отношение изменяется от 0 до 1.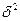 будет равна нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации.
будет равна нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации. ), т е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого признака. Чем больше значение
), т е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого признака. Чем больше значение 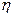 приближается к единице, тем полнее, ближе к функциональной зависимости корреляционная связь между признаками.
приближается к единице, тем полнее, ближе к функциональной зависимости корреляционная связь между признаками.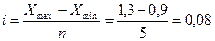 руб.
руб.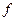


 =44, 018
=44, 018
 .
. ,
, ;
; ,
,




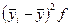



 ;
;