Решение типовых задач. №1. Для изучения расхода сырья на единицу продукции проведена двухпроцентная случайная выборка, в результате которой получены следующие обобщенные данные:
№1. Для изучения расхода сырья на единицу продукции проведена двухпроцентная случайная выборка, в результате которой получены следующие обобщенные данные:
Определить: 1) средний расход сырья на одно изделие; 2) дисперсию и среднее квадратическое отклонений; 3) коэффициент вариации; 4) с вероятностью 0, 954: предельную ошибку выборочной средней и возможные пределы расхода сырья для всей партии изделий; 5) возможные пределы удельного веса изделий с расходом сырья от 20 до 24 г.
Решение: Все необходимые расчеты представим в таблице 4.1. Таблица 4.1.
Средний расход сырья на одно изделие в выборке равен:
Вычислим дисперсию и среднее квадратическое отклонение.
Среднее квадратическое отклонение равно корню квадратному из дисперсии
Коэффициент вариации:
Предельная ошибка выборочной средней:
Следовательно, границы генеральной средней будут находиться в пределах
С вероятностью 0, 954 можно утверждать, что расход сырья на единицу продукции всей партии может изменяться от 22, 273 до 22, 927 г. Ошибка выборочной доли определяется по формуле:
Сначала определим выборочную долю (частость):
Выборка показала, что расход сырья от 20 до 24 граммов на единицу продукции приходится на 80% изделий. Определим предельную ошибку доли:
С учетом ошибки генеральная доля ожидается в границах:
Следовательно, с вероятностью 0, 954 можно утверждать, что во всей партии продукции удельный вес изделий с расходом сырья от 20 до 24 граммов ожидается в пределах не менее 72, 1 % и не более 87, 9 %. На практике применяют не только случайный отбор или механический, но и другие виды. Особое значение придается типической выборке, т.е. такой, когда генеральная совокупность разбивается на группы по изучаемому признаку, а затем из каждой группы производится отбор единиц, как правило пропорционально объему единиц в группах. Типическая выборка обеспечивает наибольшую репрезентативность. Для типической выборки предельная ошибка репрезентативности определяется по формуле где
№2. По материалам выборочного обследования 625 семей области получены следующие данные: Таблица 4.2
Выборка 2%-ная проведена по методу типического пропорционального отбора. В группах применялся механических отбор семей. С вероятностью 0, 954 определить пределы доли расходов на платные услуги жителями области. Решение: Доля расходов на платные услуги жителями области находится в пределах:
Следовательно, для решения необходимо предварительно определить среднюю долю расходов по 2 группам населения, а затем ее ошибку. Средняя доля равна:
Для расчета ошибки выборки типического отбора надо вычислить среднюю из групповых дисперсий. В графе 5 таблицы 4.2 показан расчет групповых дисперсий доли. Вычислим среднюю из них:
Теперь вычислим предельную ошибку типической выборки:
Таким образом, можно с вероятностью 0, 954 утверждать, что доля расходов населения области на платные услуги ожидается в пределах не менее 30, 7 % и не более 38, 1 %. Аналогично вычисляется ошибка типической выборки для выборочной средней (для варьирующего признака).
№3. В механическом цехе завода в десяти бригадах работает 100 рабочих. В целях изучения квалификации рабочих была произведена 20% - ная серийная бесповторная выборка, в которую вошли 2 бригады. Получено следующее распределение обследованных рабочих по разрядам:
Необходимо определить с вероятностью 0, 997 пределы, в которых находится средний разряд рабочих механического цеха.
|

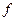
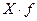
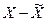

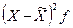
 г.
г.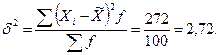
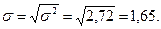
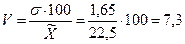 %.
%.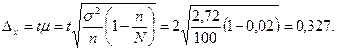
 или
или 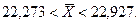
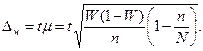
 или 80 %
или 80 % или 7.9 %
или 7.9 %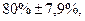 или
или 
 ,
, - средняя дисперсия из групповых дисперсий.
- средняя дисперсия из групповых дисперсий.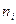
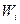
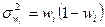
 .
.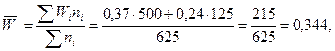 или 34, 4 %.
или 34, 4 %. .
.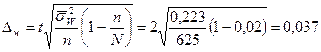 , 3, 7%;
, 3, 7%;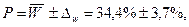 или
или 



