Решение типовых задач. №1. Имеются следующие данные о валовом сборе овощей в районе, тыс
№1. Имеются следующие данные о валовом сборе овощей в районе, тыс. ц.
Приведите ряды динамики к сопоставимому виду (сомкните ряд). Укажите вид полученного ряда динамики. Изобразите его графически.
Решение: Для приведения ряда динамики к сопоставимому виду определим для 2001 года коэффициент соотношения уровней двух рядов: 1260: 900= 1, 4.
Умножая на этот коэффициент уровни динамики в старых границах, получаем их сопоставимыми с уровнями в новых границах.
В 1999 г……………………………. В 2000 г……………………………..
Теперь представим полученные данные о валовом сборе овощей в виде ряда динамики:
Получим полный интервальный ряд динамики, который графически можно изобразить в виде столбиковой (рис 5.1.) или линейной диаграммы (статистическая кривая, рис. 5.2).
Рис.5.1 Валовой сбор овощей в 1999 – 2004 годах, тыс. ц.
Столбиковая диаграмма для графического изображения уровней ряда динамики удобна тем, что расстояние столбиков (прямоугольников) друг от друга не зависит от величины интервалов времени.
Рис. 5.2. Динамика валового сбора овощей в 1999 – 2004 годах (тыс. ц.)
Чаще всего для наглядного изображения динамики применяют линейные графики, особенно когда речь идет о наглядном изображении данных, характеризующих итоги какого-либо процесса за определенные периоды времени. Преимущество линейных графиков состоит в том, что динамика изображается в виде сплошной линии, характеризующей непрерывность процесса. Следует иметь в виду, что для графического изображения каких-либо явлений, данные которых охватывают различные периоды времени, интервалы между периодами времени (длина отрезков) при нанесении шкалы на оси абсцисс должны быть пропорциональны величинам продолжительности периодов. При построении графиков большое значение имеет выбор соотношения между размерами оси абсцисс (горизонтальной оси) и ординат (вертикальной оси). При этом следует руководствоваться так называемым правилом «золотого сечения». По этому правилу чертеж должен быть расположен в прямоугольнике, в котором длина вертикальной оси (высота графика) должна относиться к длине всей горизонтальной оси (т.е. к ширине графика) приблизительно как 5: 8. Например, если общая длина горизонтальной оси равна 16 см., то общая длина вертикальной оси должна составить Принято считать, что наиболее оптимальным для зрительного восприятия является график, выполненный на поле прямоугольной формы с соотношением сторон от 1: 1.3 до 1: 1, 5. Иногда используется и поле графика с равными сторонами, т.е. имеющее форму квадрата. При анализе рядов динамики широко применяется графический метод. Это объясняется тем, что табличное представление ряда динамики и описательные характеристики чаще всего не позволяют понять характер процесса, а по графику можно сделать определенные выводы, которые потом могут быть проверены с помощью расчетов. Графический анализ обычно задает направление дальнейшего анализа ряда динамики. В EXCEL для анализа рядов динамики (временных рядов) можно использовать средство Мастер диаграмм.
№2. Имеются данные о различной реализации хлебобулочных изделий в торговой сети города по кварталам, т:
Приведите уровни ряда к сопоставимому виду. Решение: Для приведения этого ряда динамики к сопоставимому виду определим размер среднедневной реализации с учетом числа дней торговли по кварталам, т:
Получен ряд динамики сопоставимых уровней различной реализации хлебобулочных изделий в торговой сети города по кварталам (среднедневная реализация), т:
№3. Динамика продукции (в сопоставимых ценах) характеризуется следующими данными по АО (тыс. руб.):
Определить среднегодовое производство продукции за период 2000-2004 годы. Решение: Для интервального ряда динамики средний уровень исчисляется по формуле простой средней арифметической:
№4. Имеются данные об остатках сырья и материалов на складе предприятия (тыс. руб.):
Требуется определить среднемесячный остаток сырья и материалов на складе предприятий за 1-й квартал. Решение: Для полного моментного ряда динамики средний уровень исчисляется по формуле простой средней хронологической:
№5. Имеются данные о товарных запасах розничного торгового предприятия (тыс. руб.):
Требуется исчислить среднегодовой товарный запас розничного торгового предприятия за 2004 год. Решение: Имеем неполный моментный ряд. Средний уровень такого ряда исчисляют по формуле средней хронологической взвешенной.
t – величина интервала времени (число месяцев или дней между моментами времени). Чтобы воспользоваться этой формулой, нужно превратить моментный ряд в интервальный:
Средний уровень товарных запасов за год составит:
№6. За январь месяц произошли следующие изменения в списочном составе работников предприятия, чел.:
Необходимо определить среднюю дневную списочную численность работников предприятия за январь. Решение: Запишем данные в виде ряда:
Это неполный моментный ряд динамики. Для определения среднего уровня такого ряда динамики используют среднюю арифметическую взвешенную:
у – уровни, сохраняющиеся без изменения в течение промежутков времени t; t – продолжительность каждого календарного периода с постоянной численность работающих. Для расчета средней численности работников определим продолжительность t каждого календарного периода с постоянной численностью работающих и общее число человеко-дней.
Среднедневная списочная численность работников в январе:
№7. Имеются данные о выпуске продукции «А» по месяцам отчетного года.
Необходимо рассчитать аналитические показатели ряда динамики. Решение: Простейшими показателями, которые используются при измерении скорости изменения уровней ряда динамики, являются абсолютный прирост ( В зависимости от задачи исследования абсолютные приросты, темы проста и темпы прироста в моментных и интервальных рядах с равностоящими уровнями (полных) могут быть исчислены с переменной базой сравнения (в этом случае их называют цепными) и с постоянной базой сравнения (в этом случае их называют базисными). Абсолютный прирост ( Абсолютный прирост может быть положительным, отрицательным и равным нулю. Цепной абсолютный прирост-это разность между последующим уровнем ряда и предыдущим уровнем.
Базисный абсолютный прирост – это разность между последующим уровнем и базисным.
Знак «-» свидетельствует о снижении выпуска продукции. Из полученных значений видно, что по месяцам периода происходило систематическое возрастание абсолютного снижения выпуска продукции, причем базисные и цепные показатели абсолютной убыли показывают, что в снижении выпуска продукции имело место замедление в мае месяце. Между цепными и базисными абсолютными приростами существует взаимосвязь. Каждый базисный абсолютный прирост равен сумме цепных абсолютных приростов и каждый цепной абсолютный прирост равен разности соответствующих базисных абсолютных приростов. Интенсивность изменения уровней оценивается отношением уровней. Относительными показателями динамики, характеризующими интенсивность изменения уровней являются темпы роста и прироста. Выражаются темпы роста в коэффициентах или процентах. Цепной темп роста исчисляют отношением последующего уровня у предыдущему:
Базисный – отношением каждого последующего уровня к базисному уровню
Темпы роста – только положительные числа.
Темпы роста (Т) (снижения) показывают, во сколько раз уровень данного периода или момента времени больше предыдущего или базисного уровня (если Т> 1) или какую часть предыдущего или базисного уровня составляет уровень данного периода или момента времени (если Т< 1). Между цепными и базисными темпами роста имеется взаимосвязь: - каждый базисный темп роста равен произведению соответствующий цепных темпов роста; - каждый цепной темп роста равен отношению последующего базисного к предыдущему. Темп прироста ( Цепной темп прироста ( 1) отношением цепного абсолютного прироста к предыдущему уровню
2)
Базисный темп прироста ( 1) отношением базисного абсолютного прироста к базисному уровню:
2)
Темп прироста может быть положительным, отрицательным и равным нулю. Между Пункты роста (Пр) (их иногда называют темпами наращивания) определяются двумя способами: 1) делением цепных абсолютных приростов на базисный уровень
2) разностью между базисными темпами роста:
В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в результате получая базисный темп прироста соответствующего периода. Например, сумма пунктов роста равна – 22, 9 ( Таблица 5.1
Абсолютное значение (содержание одного процента прироста (А): можно подсчитать двумя способами: 1) отношением цепного абсолютного прироста к цепному темпу прироста
2)
В полном интервальном ряду динамики средний уровень определяется по формуле простой средней арифметической:
Средний месячный выпуск продукции «А» за период с января по июнь месяц составлял:
Средний абсолютный прирост ( 1) как простая средняя арифметическая из цепных абсолютных приростов
2) как отношение базисного абсолютного прироста к числу периодов
Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался по сравнению с предыдущим уровень в среднем за единицу времени (в среднем ежемесячно, ежегодно и т.д.).
1.
2.
В течение периода с января по июнь выпуск продукции «А» в среднем ежемесячно снижался на 1, 84 тыс. шт. Средний абсолютный прирост можно использовать для экстраполяции и интерполяции. Под экстраполяцией понимают нахождение уровней за пределами ряда. Экстраполяция, проводимая в будущее, называется перспективной, или прогнозированием, а в прошлое-ретроспективной. При прогнозировании уровней явления на базе ряда динамики с постоянными абсолютными приростами (
t - срок прогноза;
Чем короче срок экстраполяции, тем более точные и надежные результаты дает прогноз. При интерполяции применяется формула:
Средний темп роста ( Определяется по формуле средней геометрической двумя способами:
В примере 7: 1.
2. Средний темп прироста ( Средний темп прироста характеризует среднюю интенсивность изменения, т.е. среднюю относительную скорость изменения уровня. Определяется по формулам:
В примере 7:
Прогнозирование уровня явления на базе ряда динамики со стабильными темпами роста (
Среднее абсолютное значение одного процента прироста за период определяется по формуле простой средней арифметической из абсолютных значений одного процента прироста.
В примере 7:
Коэффициент опережения. При характеристике процесса опережения различных явлений можно сопоставлять только относительные показатели динамики, исчисленные за один и тот же период. Поэтому ряды динамики, уровни которых непосредственно несопоставимы, приводят сначала к одному основанию, т.е. выражают в виде базисных темпов роста, а затем на основе темпов роста вычисляют коэффициенты относительного опережения по формуле
где
№8. Имеются относительные показатели естественного движения населения района в расчете на 1000 чел. населения.
Определить коэффициенты опережения. Решение: Уровни этих рядов динамики непосредственно несопоставимы из – за возрастной структуры населения, которая различна в разные годы. В данном случае несопоставимость устраняют приведением рядов динамики к одному основанию, то есть расчетом базисных темпов роста. Расчет базисных темпов роста осуществляется в табл. 5.2. гр. 3, 4. Таблица 5.2
Коэффициент опережения по формуле
Следовательно, смертность в районе в 2004 году росла в 1, 651 раза быстрее, чем рождаемость. Если за период 2000 – 2004 годы среднегодовой темп снижения рождаемости составлял 0, 946, а среднегодовой темп роста смертности - 1, 072, то коэффициент опережения можно определить следующим образом
Следовательно, за период 2000 – 2004 смертность в районе росла в1.651 раза быстрее, чем рождаемость.
№9. Численность населения региона возросла за период с 1.1. 2003 по 1.01.2005 на 5, 3%, при этом удельный вес мужского населения за этот период увеличился с 41, 9 до 45, 4 %. Определить показатели динамики численности мужского и женского населения региона. Решение: Исходим из следующих соотношений:
численность общая удельный женского = численность Х вес населения населения женщин
численность общая удельный мужского = численность Х вес населения населения мужчин
Изменения численности населения характеризуется темпами роста (Т). По условию задачи темп роста общей численности населения за рассматриваемый период составил:
Темп роста удельного веса мужского населения:
Аналогично определяем темп роста удельного веса женского населения:
На основе приведенных соотношений получим:
1)
2) где Следовательно, численность мужского населения региона возросла за указанный период на 14, 1%, а женского снизилась на 1 %.
№10 Имеются данные о выпуске продукции предприятия по месяцам:
Требуется выявить основную тенденцию выпуска продукции с помощью скользящей средней. Решение: Если колебания ряда не имеют волнообразного характера, то для вычисления скользящей средней следует брать в «укрупненный» интервал нечетное количество уровней ряда (три, пять, и т.д.). Скользящие средние для укрупненного интервала, охватывающего три уровня, определяются по следующим формулам:
Результаты расчета трехмесячных скользящих средних представим в таблице 5.3 гр.3: Таблица 5.3
В гр.1 таблицы 5.3 нет четкой тенденции роста производства продукции. Наряду с ростом имеется в отдельные месяцы и снижение производства продукции. Сглаженные значения (табл.5.3 гр.3) отчетливо отражают основную тенденцию – систематическое увеличение выпуска продукции на предприятии в течении года.
№11 Имеются данные о выпуске продукции предприятием:
Требуется выявить основную тенденцию выпуска продукции за январь – сентябрь методом аналитического выравнивания ряда динамики по уравнению прямой и построить график. Рассчитать интервальный прогноз выпуска продукции на октябрь месяц с вероятностью 0, 95. Решение: Уравнение прямой линии выражается формулой:
Для определения величины параметров
где у - величины уровней эмпирического (фактического) ряда динамики; n - количество уровней эмпирического ряда динамики; t – временные показатели (месяцы, кварталы, годы).
Так как количество уровней в выравниваемом ряде динамики – нечетное, то для упрощения расчетов временные показатели (t) обозначим следующим образом:
В этом случае
Значения параметров уравнения прямой определяются по формулам:
Таблица 5.4.
Рассчитаем величины параметров:
По исчисленным параметрам составляем уравнение прямой выравненного ряда динамики:
Полученное уравнение показывает, что выпуск продукции предприятия за исследуемый период увеличивался в среднем на 2, 908 тыс. руб. в месяц. Таким образом, величина параметра а1 уравнения прямой характеризует среднюю величину абсолютного прироста выравненного ряда динамики. На основании этого уравнения определим величины уровней выравненного ряда динамики, а именно: для января
для февраля
для сентября Для проверки правильности рассчитанных величин уровней выравненного ряда динамики используются следующие сопоставления. Сумма значений эмпирического ряда
В нашем примере Кроме того, любой уровень выравненного ряда Так, в нашем примере:
Выравненный по прямой ряд
Фактический ряд динамики
Рис.5.3. Выравнивание ряда динамики по прямой
Уравнение тренда можно использовать для интерполяции (чтобы найти недостающие члены ряда) и для экстраполяции (для прогноза – для предсказания дальнейшего развития). Для прогнозирования возможного выпуска продукции в октябре месяце в уравнение тренда подставим t=5, получим:
Это точечный прогноз. На практике результат экстраполяции прогнозируемых уровней обычно выполняется интервальными оценками. Для определения границ интервалов используется формула:
где
|





 см.
см. тыс. руб. т.е. в течение периода с 2000 по 2004 годы АО в среднем ежегодно производило продукции на 11015 тыс. руб.
тыс. руб. т.е. в течение периода с 2000 по 2004 годы АО в среднем ежегодно производило продукции на 11015 тыс. руб. тыс. руб.
тыс. руб. , где
, где - средние уровни интервала между датами;
- средние уровни интервала между датами; )
)




 тыс. руб.
тыс. руб. , где
, где
 чел.
чел. ), темп роста (
), темп роста ( ), темп прироста (
), темп прироста ( ), а также абсолютное значение одного процента прироста (А), пункты роста.
), а также абсолютное значение одного процента прироста (А), пункты роста. . Подсчитываем в гр. 2 табл. 5.1.
. Подсчитываем в гр. 2 табл. 5.1. . Подсчитываем в гр. 3 табл.5.1.
. Подсчитываем в гр. 3 табл.5.1. (расчет см. гр.4. табл.5.1).
(расчет см. гр.4. табл.5.1). (расчет см. гр.5. табл.5.1).
(расчет см. гр.5. табл.5.1).
 ) (сокращения) показывает, на сколько процентов уровень данного периода или момента времени больше (или меньше) предыдущего или базисного уровня.
) (сокращения) показывает, на сколько процентов уровень данного периода или момента времени больше (или меньше) предыдущего или базисного уровня.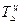 ) определяется двумя способами:
) определяется двумя способами:
 или
или  (расчет см. гр.6. табл.5.1.)
(расчет см. гр.6. табл.5.1.) ) определяется двумя способами:
) определяется двумя способами:

 (расчет см. гр. 7 табл.5.1.)
(расчет см. гр. 7 табл.5.1.) взаимосвязи не существует, их нельзя суммировать и перемножать.
взаимосвязи не существует, их нельзя суммировать и перемножать.
 (расчет см. гр.8. табл.5.1.)
(расчет см. гр.8. табл.5.1.) ), соответствует темпу прироста выпуска продукции в июне по сравнению с январем.
), соответствует темпу прироста выпуска продукции в июне по сравнению с январем. или
или

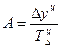 или
или




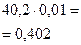

 =0, 771
=0, 771

 ;
; (расчет см. гр. 9 табл.5.1.)
(расчет см. гр. 9 табл.5.1.) .
.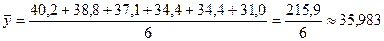 тыс.шт.
тыс.шт.
 .
. тыс. шт.
тыс. шт. тыс.шт.
тыс.шт. ) применяется формула:
) применяется формула: , где
, где - прогнозируемый уровень; n+t – номер этого уровня (года);
- прогнозируемый уровень; n+t – номер этого уровня (года);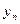 - конечный уровень базисного ряда динамики за который рассчитан
- конечный уровень базисного ряда динамики за который рассчитан  ;
; .
. ) показывает, во сколько раз увеличивался (или снижался) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.п.).
) показывает, во сколько раз увеличивался (или снижался) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.п.).
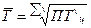 , где
, где 


 , следовательно, в течение периода с января по июнь выпуск продукции «А» ежемесячно составлял 0, 949 от предыдущего.
, следовательно, в течение периода с января по июнь выпуск продукции «А» ежемесячно составлял 0, 949 от предыдущего. ) (снижения), выраженный в процентах, показывает, на сколько процентов увеличивался (или уменьшался) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно).
) (снижения), выраженный в процентах, показывает, на сколько процентов увеличивался (или уменьшался) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно). или
или  .
. , следовательно, выпуск продукции «А» в течение периода с января по июнь в среднем ежемесячно снижался на 5, 1 %.
, следовательно, выпуск продукции «А» в течение периода с января по июнь в среднем ежемесячно снижался на 5, 1 %. ) осуществляется по формуле:
) осуществляется по формуле: .
. .
. шт.
шт. ,
, - базисные темпы роста первого и второго рядов соответственно.
- базисные темпы роста первого и второго рядов соответственно.








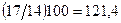

 показывает, во сколько раз быстрее растет уровень одного ряда динамики по сравнению с уровнем другого ряда динамики. Так, для 2004 года коэффициент опережения равен:
показывает, во сколько раз быстрее растет уровень одного ряда динамики по сравнению с уровнем другого ряда динамики. Так, для 2004 года коэффициент опережения равен:






 ,
,  - соответственно темп роста численности мужчин и женщин.
- соответственно темп роста численности мужчин и женщин.
 и т.д.
и т.д.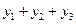 )
)
 )
)
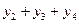 )
)
 )
)
 )
)
 )
)
 )
)
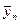 )
)
 .
. и
и  используются нормальные уравнения способа наименьших квадратов, которые в данном случае принимают следующий вид:
используются нормальные уравнения способа наименьших квадратов, которые в данном случае принимают следующий вид: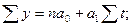
 ,
, и система нормальных уравнений принимает следующий вид:
и система нормальных уравнений принимает следующий вид: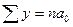
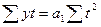 .
. ,
,  .
.






 тыс. шт.;
тыс. шт.; тыс.шт.;
тыс.шт.; тыс.шт.
тыс.шт. должна совпадать с суммой исчисленных значений выравненного ряда
должна совпадать с суммой исчисленных значений выравненного ряда  , т.е.
, т.е.  можно получить путем прибавления величины параметра а1 к исчисленному значению предшествующего уровня выравненного ряда.
можно получить путем прибавления величины параметра а1 к исчисленному значению предшествующего уровня выравненного ряда. тыс. шт.
тыс. шт. тыс.шт.
тыс.шт. тыс.шт. и т.д. см. гр.6 Табл. 5.4.
тыс.шт. и т.д. см. гр.6 Табл. 5.4. Построим график 5.3:
Построим график 5.3:
 динамики
динамики


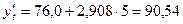 тыс. шт.
тыс. шт. ,
, - коэффициент доверия по распределению Стьюдента;
- коэффициент доверия по распределению Стьюдента; - остаточное среднее квадратическое о
- остаточное среднее квадратическое о


