Решения типовых задач
№1. Имеются выборочные данные по 15 коммерческим банкам региона:
Построить однофакторную регрессионную линейную модель. Решение: Предположим, что между объемом собственных средств и привлеченных средств существует линейная корреляционная связь, которую можно выразить уравнением прямой вида Для определения параметров Таблица 7.7 Расчетные значения, необходимые для исчисления
Продолжение таблицы 7.7
Пользуясь расчетными значениями (см. Табл. 7.7.), подсчитаем параметры для данного уравнения регрессии:
Следовательно, регрессионная модель объема привлеченных средств по собственным средствам банков для данного примера может быть записана в виде следующего уравнения регрессии:
Это уравнение характеризует зависимость среднего объема привлеченных средств банков от собственных средств. Расчетные значения Если параметры регрессионного уравнения подсчитаны верно, то должно соблюдаться равенство сумм теоретических и эмпирических значений объема привлеченных средств, В нашем уравнении регрессии параметр Если исследуемые признаки имеют разные единицы измерения, для оценки влияния факторного признака на результативный применяется коэффициент эластичности. Коэффициент эластичности рассчитывается для каждой точки по формуле:
где Он показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1%. Средний коэффициент эластичности определяется для уравнения прямой по формуле:
Если зависимость величин результативного признака у от значений факторного признака х имеет форму гиперболической зависимости, то есть характеризуется корреляционным уравнением
Производим замену переменных
Параметры уравнения гиперболы можно вычислить по формулам:
Гиперболическая форма корреляционной связи используется при изучении зависимости уровня себестоимости единицы продукции от объема выпуска продукции. Если зависимость величин результативного признака у от значений факторного признака х характеризуется корреляционным уравнением параболы второй степени И парабола, и прямая являются частным случаем полинома n-ой степени вида Систему уравнений для определения параметров
|

 .
. и
и  методом наименьших квадратов воспользуемся формулами
методом наименьших квадратов воспользуемся формулами  ,
,  .
.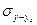 ,
,  ,
, 
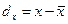

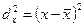

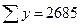

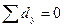
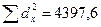
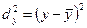

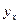


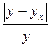
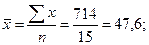
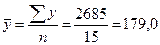 .
.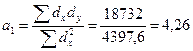 ,
,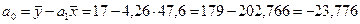 .
. .
. , а сумма разностей между эмпирическими и теоретическими значениями объема привлеченных средств должна быть равна 0
, а сумма разностей между эмпирическими и теоретическими значениями объема привлеченных средств должна быть равна 0 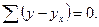 (гр.10. табл. 7.7).
(гр.10. табл. 7.7).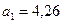 показывает, что с увеличением объема собственных средств одного банка на 1 млн. руб. объем привлеченных средств возрастает в среднем на 4, 26 млн. руб.
показывает, что с увеличением объема собственных средств одного банка на 1 млн. руб. объем привлеченных средств возрастает в среднем на 4, 26 млн. руб.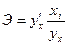 ,
,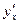 - первая производная уравнения регрессии.
- первая производная уравнения регрессии. .
.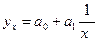 , то для определения параметров
, то для определения параметров 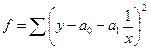 , по
, по 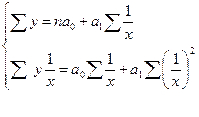 .
.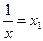 , получаем следующую систему нормальных уравнений:
, получаем следующую систему нормальных уравнений: .
.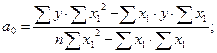

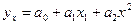 , то это параболическая зависимость.
, то это параболическая зависимость. .
. можно найти, приравнивая нулю частные производные от
можно найти, приравнивая нулю частные производные от 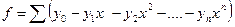 по
по 


