Проверка значимости показателей тесноты корреляционной связи
Показатели тесноты связи, исчисленные по данным небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки из значимости (надежности, существенности). Для оценки значимости коэффициента корреляции применяется t–критерий Стьюдента, который определяется по формуле:
где Вычисленное по формуле значение Если Для оценки значимости индекса корреляции R применяется F -критерий Фишера. Фактическое значение критерия
где m– число параметров уравнения регрессии. Величина Если
Табличное значение t–критерия с уровнем значимости 0, 05 и числом степеней свободы Оценка индекса корреляции R=0, 973 осуществляется по F–критерию. Определяется фактическое значение:
При уровне значимости Вычислим ошибку аппроксимации по формуле:
Так как параметры уравнения регрессии значимы, уравнение значимо, показатели тесноты значимы, ошибка аппроксимации равна 11, 3 %, коэффициент детерминации равен 0, 947, то построенная регрессионная модель зависимости объема привлеченных средств от объема собственных средств
|

 ,
, - число степеней свободы при данном уровне значимости
- число степеней свободы при данном уровне значимости 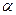 и объеме выборки n.
и объеме выборки n. сравнивается с критическим
сравнивается с критическим  .
. определяется по формуле:
определяется по формуле: ,
, , которое определяется по таблице F –критерия с учетом принятого уровня значимости а и числа степеней свободы
, которое определяется по таблице F –критерия с учетом принятого уровня значимости а и числа степеней свободы  и
и  .
. .
. равно 2, 161. Фактическое значение
равно 2, 161. Фактическое значение  .
. и
и  табличное значение
табличное значение  .
. может быть использована для анализа и прогноза.
может быть использована для анализа и прогноза.


