Краткая теория. Все вещества при изучении их магнитных свойств называются магнетиками и по взаимодействию с внешним магнитным полем делятся на диамагнетики
Все вещества при изучении их магнитных свойств называются магнетиками и по взаимодействию с внешним магнитным полем делятся на диамагнетики, парамагнетики и ферромагнетики. Магнитная проницаемость у диамагнетиков и парамагнетиков мало отличается от единицы и, поэтому они относятся к слабо магнитным веществам. У ферромагнетиков магнитная проницаемость значительно больше единицы. Все ферромагнетики характеризуются: 1. кристаллическим строением; 2. нелинейной зависимостью магнитной индукции 3. большим значением магнитной проницаемости, а также ее существенной и нелинейной зависимостью от напряженности внешнего магнитного поля, т.е. 4. способностью намагничиваться до насыщения при обычных температурах уже в слабых магнитных полях; 5. магнитным гистерезисом – зависимостью магнитных свойств от предшествующего состояния (рис. 4.2); 6. точкой Кюри, т.е. температурой
Для полного размагничивания образца ( Увеличивая магнитное поле можно перемагнитить образец до насыщения (точка 4). Если теперь напряженность магнитного поля уменьшать, то индукция магнитного поля образца будет изменяться по кривой 4-5-6-1. Таким образом, при действии на ферромагнетик переменного магнитного поля намагниченность образца, а, следовательно, и магнитная индукция Основными характеристиками петли гистерезиса являются: - остаточная индукция - коэрцитивная сила - площадь петли
Значение напряженности
где
Здесь На основании 1.4 и рисунка 4.3. получаем, что отклонение электронного луча по оси «Х» в осциллографе пропорционально напряженности магнитного поля в образце. ЭДС индукции
Отсюда
где
Здесь Таким образом, отклонение луча по оси «Y» на экране осциллографа пропорционально магнитной индукции в образце. В результате на экране осциллографа получается петля гистерезиса. За один период изменения намагничивающего тока луч на экране опишет полную петлю, а за каждый последующий период в точности повторит ее. Поэтому на экране будет видна неподвижная петля гистерезиса. Полную удельную мощность потерь в образце можно найти по формуле
где
Здесь Удельную мощность потерь на вихревые токи
где
Здесь Удельную мощность потерь на гистерезис
|

 от напряженности внешнего магнитного поля
от напряженности внешнего магнитного поля  (рис. 4.1а).
(рис. 4.1а). (рис. 4.1б) и температуры;
(рис. 4.1б) и температуры; , выше которой материал теряет свои ферромагнитные свойства.
, выше которой материал теряет свои ферромагнитные свойства. Рассмотрим более подробно процесс перемагничивания ферромагнетика. При медленном нарастании внешнего магнитного поля
Рассмотрим более подробно процесс перемагничивания ферромагнетика. При медленном нарастании внешнего магнитного поля  Если после достижения магнитного насыщения образец привести в исходное состояние путем уменьшения намагничивающего поля
Если после достижения магнитного насыщения образец привести в исходное состояние путем уменьшения намагничивающего поля  оказывается равной
оказывается равной  (точка 2) (см. рис. 4.2). Величина
(точка 2) (см. рис. 4.2). Величина  ) точка 3 (рис.4.2) нужно приложить магнитное поле, направленное в противоположную сторону. Напряженность магнитного поля
) точка 3 (рис.4.2) нужно приложить магнитное поле, направленное в противоположную сторону. Напряженность магнитного поля  , при которой индукция магнитного поля в образце обращается в нуль, получила название коэрцитивной силы (0-3, 0-6 – на рисунке 4.2).
, при которой индукция магнитного поля в образце обращается в нуль, получила название коэрцитивной силы (0-3, 0-6 – на рисунке 4.2). - характеризующая потери энергии на перемагничивание ферромагнетика.
- характеризующая потери энергии на перемагничивание ферромагнетика.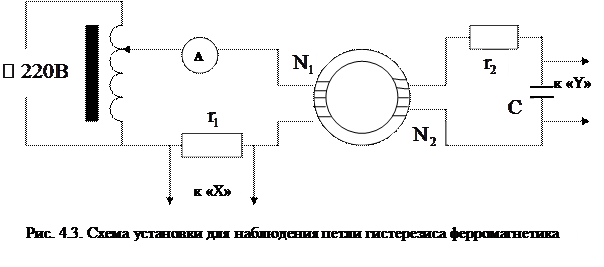 Для наблюдения петли гистерезиса используется схема, изображенная на рисунке 4.3.
Для наблюдения петли гистерезиса используется схема, изображенная на рисунке 4.3. , 1.4
, 1.4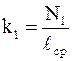 . 2.4
. 2.4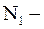 число витков в намагничивающей обмотке,
число витков в намагничивающей обмотке,  длина тороида по средней линии,
длина тороида по средней линии,  действующее значение намагничивающего тока.
действующее значение намагничивающего тока. , наводимая во вторичной обмотке с числом витков
, наводимая во вторичной обмотке с числом витков  может быть определена по формуле
может быть определена по формуле . 3.4
. 3.4 , 4.4
, 4.4 . 5.4
. 5.4 - емкость конденсатора,
- емкость конденсатора, 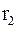 - сопротивление,
- сопротивление, 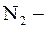 число витков во вторичной обмотке,
число витков во вторичной обмотке,  ЭДС индукции во вторичной обмотке,
ЭДС индукции во вторичной обмотке,  площадь поперечного сечения образца.
площадь поперечного сечения образца. , 6.4
, 6.4 . 7.4
. 7.4 площадь петли гистерезиса,
площадь петли гистерезиса, 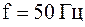 - частота переменного тока,
- частота переменного тока,  - число витков в первичной и вторичной обмотке,
- число витков в первичной и вторичной обмотке,  - максимальное отклонение электронного луча на экране осциллографа по оси «
- максимальное отклонение электронного луча на экране осциллографа по оси « » и по оси «
» и по оси « ».
».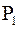 в образце рассчитывают по формуле
в образце рассчитывают по формуле , 8.4
, 8.4 9.4
9.4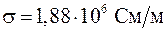 - удельная проводимость ферромагнетика,
- удельная проводимость ферромагнетика,  - плотность образца,
- плотность образца,  - толщина листа стали образца,
- толщина листа стали образца, 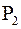 определяют как разность между полной удельной мощность потерь и удельной мощностью потерь на вихревые токи, т.е.
определяют как разность между полной удельной мощность потерь и удельной мощностью потерь на вихревые токи, т.е. . 10.4
. 10.4


