Задача №4. Динамический расчет компрессора
Исходные данные: Необходимые исходные данные можно получить, решив задачу №2, 3. Последовательность решения: В ходе динамического расчета определяются силы и моменты, действующие в компрессоре.
Рисунок 13. – Схема кривошипно-шатунного механизма. Суммарная свободная сила действует по оси цилиндра:
где: Сила от давления пара в цилиндре определяется разностью давлений со стороны крышки цилиндра
Сила инерции поступательно движущихся масс:
где: Силу трения поступательно движущихся частей условно принимают постоянной:
Сила трения направлена против движения и меняет свой знак в мертвых точках. Суммарную свободную силу можно разложить на две составляющие: · силу, действующую по оси шатуна: · силу, действующую на стенку цилиндра: Силу · тангенциальную силу, действующую перпендикулярно к кривошипу: · радиальную силу, действующую по кривошипу: Направление действующих сил принято положительным, следовательно, при положительном значении, силы Результаты динамического расчета используют при расчете на прочность деталей компрессора, подшипников на износ, для проектирования системы смазки и определения неуравновешенных сил и моментов. Силы, действующие в компрессоре, изменяются в зависимости от угла поворота кривошипа. Для определения максимальных, минимальных и средних за цикл значений нагрузки деталей кривошипно-шатунного механизма строят диаграммы сил, позволяющих оценить характер нагружения. Сила инерции поступательно движущихся масс:
где:
где: Масса поршня и шатуна определяется из конструктивных соображения в зависимости от полученного диаметры поршня.
Результаты расчета сил инерции в зависимости от угла поворота кривошипа приведены в таблице 3. Таблица 3
|


 ,
, – сила от давления пара в цилиндре;
– сила от давления пара в цилиндре;  – сила инерции поступательно движущихся масс;
– сила инерции поступательно движущихся масс;  – сила трения поступательно движущихся частей.
– сила трения поступательно движущихся частей.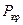 и со стороны вала
и со стороны вала  :
: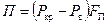 .
. ,
, – масса поступательно движущихся частей (поршня, поршневого пальца, 1/3 массы шатуна), кг;
– масса поступательно движущихся частей (поршня, поршневого пальца, 1/3 массы шатуна), кг; 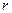 – радиус кривошипа, м;
– радиус кривошипа, м;  – угловая скорость вала, с-1;
– угловая скорость вала, с-1;  – угол поворота кривошипа от верхней мертвой точки;
– угол поворота кривошипа от верхней мертвой точки; 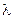 – отношение радиуса кривошипа к длине шатуна, обычно
– отношение радиуса кривошипа к длине шатуна, обычно 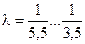 .
. .
. ;
; .
. , приложенную к шатунной шейке можно разложить на:
, приложенную к шатунной шейке можно разложить на: ;
;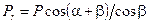 .
. ,
, 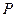 – вызывают сжатие шатуна, сила
– вызывают сжатие шатуна, сила 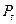 – направлена против вращения вала, сила
– направлена против вращения вала, сила  – к оси вращения вала.
– к оси вращения вала. ,
, – сила инерции первого порядка;
– сила инерции первого порядка;  – сила инерции второго порядка.
– сила инерции второго порядка. ,
, – масса поршня в сборе с поршневым пальцем;
– масса поршня в сборе с поршневым пальцем; 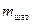 – масса шатуна.
– масса шатуна. , рад/с.
, рад/с. м – радиус кривошипа.
м – радиус кривошипа.


