Пример №1. Анализ исходной системы
Анализ исходной системы и дальнейший выбор корректирующего фильтра будет продемонстрирован на конкретном примере системы первого порядка астатизма, заданной передаточной функцией системы в разомкнутом состоянии:
Анализ системы удобно разбить на ряд этапов:
1. Определение дискретной передаточной функции W (z) системы в разомкнутом состоянии. W (z) – это результат применения Z-преобразования, к передаточной функции W (s). Используются таблица преобразований Лапласа и Z-преобразований, содержащаяся в приложении. Данные таблицы ограничены, поэтому в рассматриваемом случае W (s) представляется суммой простейших слагаемых, над каждым из которых можно осуществить Z-преобразование.
Таким образом,
Два уравнения относительно переменных A и B формируются после приравнивания коэффициентов числителя при одинаковых степенях переменной s: A/T = 1; A+B = τ; следовательно, A = T, B = - (T - τ) и передаточная функция W (s) представляется в виде
В соответствии с таблицей Z-преобразований получим
После приведения к общему знаменателю для рассматриваемого примера получим
2. Анализ устойчивости по расположению корней характеристического уравнения на Z-плоскости. Z-передаточная функция системы в замкнутом состоянии равна
Знаменатель этой передаточной функции A (z) является характеристическим полином системы. Приравняв его нулю и решая полученное характеристическое уравнение, получим два комплексно-сопряженных корня
Границей устойчивости на Z-плоскости является окружность единичного радиуса с центром в начале координат. Система устойчива если все корни характеристического уравнения находятся внутри этой окружности. В приведенном примере модуль этих корней меньше единицы, следовательно, система устойчива, но запас устойчивости ее невелик. 3. Показатели качества, определяемые по виду логарифмической амплитудно-частотной характеристике (ЛАХ). Как уже отмечалось, для анализа дискретных систем часто применимы методы, разработанные для исследования непрерывных систем. Особенно это касается применения ЛАХ для анализа качества системы. Частотные характеристики – это характеристики комплексного коэффициента передачи системы в разомкнутом состоянии. Чтобы их получить, предварительно в выражении () необходимо осуществить замену переменной
Комплексный коэффициент передачи системы в разомкнутом состоянии
Выражение (13) можно представить в виде произведения комплексных коэффициентов передачи четырех типовых звеньев
1. интегрирующего звена с коэффициентом усиления K = 1000 1/с, 2. инерционного звена с постоянной времени T = 0, 0503 с, 3. устойчивого форсирующего звена с постоянной времени t1 = 0, 001с, 4. неустойчивого форсирующего звена с постоянной времени t2 = 0, 488× 10-3 с.
Первые три первых звена являются типовыми. Построение ЛАХ для них рассмотрено в разделе. Амплитудно-частотная характеристика неустойчивого форсирующего звена совпадает с аналогической характеристикой устойчивого форсирующего звена, а его фазочастотная характеристика – с характеристикой инерционного звена L 4(λ) = L 3(λ), φ 4(λ) = - φ 3(λ). () Таким образом, фазо-частотные характеристики последних двух звеньев уравновешиваются (φ 3, 4(λ) = 0). Изобразив ЛАХ всех четырех звеньев и графически просуммировав их, получим ЛАХ исследуемой системы в разомкнутом состоянии. Для проверки выполнения пункта 4 технического задания (см. раздел 4.2.1.) на график логарифмической амплитудной характеристики наносится изображение запретной зоны по точности. Рассматриваемая система является астатической системой первого порядка астатизма. Запретная зона по точности соответствует зоне, изображенной на рис. 3.10. b. Координаты контрольной точки вычисляются по формулам: l x = A 1/ B 1 = 1 1/с, Анализ изображенных на рис. 4.7 характеристик исходной системы позволяет сделать следующие заключения: 1. Характерными частотами исследуемой системы (определяются по графикам ЛАХ) являются: · lд = 2/ T 0 = 103 1/с – песевдочастота, связанная с дискретизацией системы по времени; · lср = 141 1/с – псевдочастота среза, определяемая соотношением L (lср) = 0; · lкр = ¥ – критическая псевдочастота, j(lкр) = - 180°. · Запасы устойчивости: по амплитуде D L = 40 дБ (D L = | L (lкр)|), по фазе Dj = 10° (Dj = 180° - |j(lср)|).
2. Для рассматриваемой системы псевдочастота среза lср существенно меньше псевдочастоты lд = 2/ T 0, связанной с дискретизацией. Поэтому в области псевдочастот lср < 2/ T 0 приведенные на рис. 4.7 характеристики дискретной системы практически полностью совпадают с соответствующими характеристиками непрерывной системы с передаточной функцией W нч(s). В области псевдочастот lср > 2/ T 0 характеристики дискретной и непрерывной систем существенно различаются. В этом случае для анализа дискретной системы разработаны другие методы (например, использование уравнений в конечных разностях). 3. Изучаемая система устойчива, поскольку lср < lкр. 4. Запас устойчивости по фазе не удовлетворяет техническим условиям (Dj = 10°< 30°). 5. Логарифмическая амплитудно-частотная характеристика L = L (l) пересекает запретную зону по точности на участке с наклоном - 20 дБ/дек, следовательно, исходная система не удовлетворяет требованиям точности по скорости входного воздействия. 6. Поскольку ломаная кривая L (l) на псевдочастоте lср имеет наклон - 40 дБ/дек, есть все основания полагать, что переходный процесс системы имеет колебательный характер.
|

 (4.5)
(4.5)
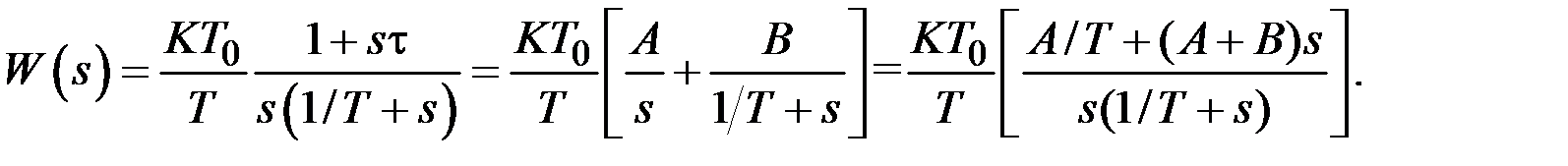

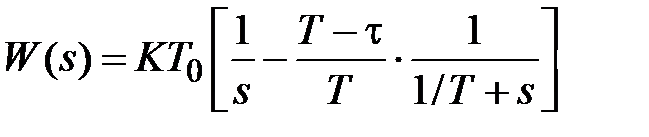 . ()
. () .
. . ()
. () .()
.() .
. , т.е. перейти к передаточной функции W (w), как функции переменной w
, т.е. перейти к передаточной функции W (w), как функции переменной w ()
() – это передаточная функция W (w), когда
– это передаточная функция W (w), когда  , где l – псевдочастота, λ д =
, где l – псевдочастота, λ д =  =0, 001 1/с – пведочастота дискретизации.
=0, 001 1/с – пведочастота дискретизации. (13)
(13)


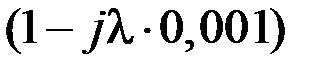 :
: , L (l x) = 20× lg(Ax) = 66 дБ.
, L (l x) = 20× lg(Ax) = 66 дБ.


