Пример №2. Анализ и коррекция цифроаналоговой системы
Задана система, передаточная функция непрерывной части которой равна
T 0 = 0, 002 c, K = 200, T 1 = 0, 05 c, T 2 = 0, 002 c, A 0 = 0, 005, B 0 = 0, 001.
Согласно выражению (4.2) передаточная функция системы в разомкнутом состоянии имеет вид
После некоторых преобразований, связанных с представлением функции W (s) как сумму двух слагаемых имеем для рассматриваемого примера
Применяя Z-преобразование, используя таблицу приложения, получим
Далее требуется применить W -преобразование с помощью подстановки
Ниже будет показано, что для изучения показателей качества изучаемой цифровой системы применимы все методы, разработанные для анализа аналоговых систем, основанные на изучении частотных характеристик. Для построения графиков логарифмических частотных характеристик с помощью подстановки
Графическое изображение ЛАХ исходной системы представлено на рис. 4.8.

Координаты запретной зоны по точности: λ x= A 0/ B 0 = 5 1/c, A (λ x)= 1/ A 0 = 200, L (λ x) = 46 Дб.
Исходная система неустойчивая, поскольку график кривой L = L (λ) проходит выше оси λ. Для ее коррекции применяется фильтр с запаздыванием по фазе (см. рис.4.8) с параметрами: K кор = 1, tкор = 0, 02 с, T кор = 0, 5 с. Параметры фильтра подбирались из следующих соображений: · Для того чтобы удовлетворять требованиям устойчивости необходимо, чтобы кривая L = L (λ) на больших частотах (λ > λ д = 1000 1/с) проходила ниже оси псевдочастот. Если кроме того требуется обеспечить запас устойчивости D L рез не меньше 14 дБ, необходимо на больших частотах понизить коэффициент усиления системы не менее чем на 20 дБ. Следовательно (см. рис. 4.8), постоянные времени tкор и T кор должны различаться в 10 раз. · Построенная на рис. 4.8 запретная зона по точности показывает, что амплитудная характеристика L = L (λ) не пересекает запретной зоны по точности. Следовательно, чтобы результирующая система удовлетворяла требованиям технического задания по точности нет необходимости увеличивать коэффициент усиления фильтра. Поэтому он принят равным единице K кор = 1. · Для уменьшения колебательности желательно, чтобы в районе псевдочастоты · Следует учитывать, что при применении фильтра с запаздыванием по фазе уменьшается частота среза
Итак, результирующая система после применения фильтра с запаздыванием по фазе обладает следующими свойствами: 1. Параметры результирующей системы, определяемые по виду логарифмических частотных характеристик:
2. Анализ рассматриваемой цифроаналоговой системы может проводиться с применением всех методов, разработанных для анализа аналоговых систем, поскольку 3. Результирующая система устойчива, так как 4. Запасы устойчивости по амплитуде и по фазе удовлетворяют техническому заданию D L рез = 14 дБ, Djрез = 42° > 30°. 5. Амплитудная характеристика L = L (λ) не пересекает запретную зону по точности. Следовательно, результирующая система удовлетворяет требованиям технического задания по точности. Контрольные вопросы 1. Какие функции, выполняют элементы цифроаналоговых систем: АЦП, ДФ, ЦАП? Их математические модели. 2. Какие показатели, характеризующие качество дискретной системы, формируют техническое задание на проектирование? 3. Какие характерные псевдочастоты определяются по ЛАХ системы? 4. Сформулировать условие, при выполнении которого для анализа дискретной системы можно применять методы, разработанные для аналоговых систем. 5. Условия устойчивости цифроаналоговых систем. 6. Как повысить точность системы? 7. Как различаются корректирующие фильтры с опережением и запаздыванием по фазе? Их преимущества и недостатки. 8. Как псевдочастота среза системы lср влияет на быстродействие системы?
|

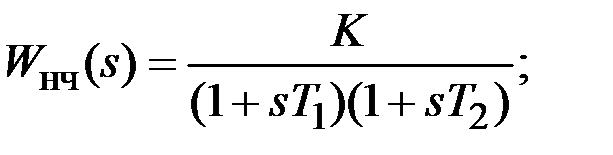
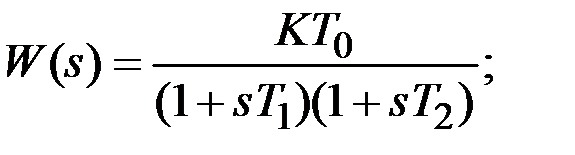
 ,
, 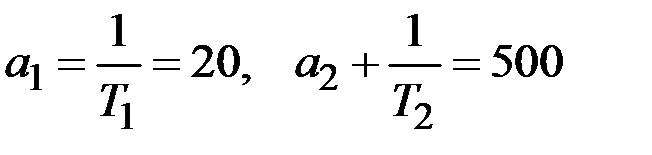 .
.
 .
.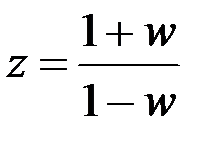 . Таким образом, после некоторых преобразований получим
. Таким образом, после некоторых преобразований получим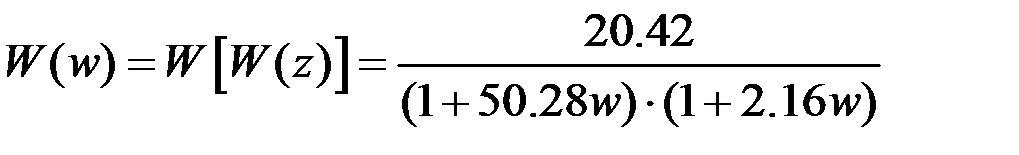 .
. переходят к комплексному коэффициенту передачи системы в разомкнутом состоянии.
переходят к комплексному коэффициенту передачи системы в разомкнутом состоянии.
 наклон амплитудной характеристики был равен - 20 дБ/дек.
наклон амплитудной характеристики был равен - 20 дБ/дек. , т.е. уменьшается полоса пропускания системы и, следовательно, и ее быстродействие.
, т.е. уменьшается полоса пропускания системы и, следовательно, и ее быстродействие. = 400 1/с,
= 400 1/с,  , D L рез = 14 дБ, Djрез = 42°.
, D L рез = 14 дБ, Djрез = 42°. < λ д = 1000 1/с.
< λ д = 1000 1/с. <
<  .
.


