Собственная информация. Взаимная информация
Пример 5. На экране индикатора РЛС, представляющего поле с 10 вертикальными и 10 горизонтальными полосами, появляется изображение объекта в виде яркостной отметки. Все положения объекта равновероятны. Определить количество информации, содержащееся в сообщениях: а) объект находится в 46-м квадрате экрана; б) объект находится в 5-й горизонтальной строке экрана; в) объект находится в 6-м вертикальном столбце и 3-й горизонтальной строке экрана. Решение. а) Пусть Собственная информация в этом сообщении по формуле (4.2) [1] равна По условию задачи
б) Вероятность события
в) Вероятность события
Пример 6. Рассматривается ансамбль сообщений, приведенный в табл. 2. Таблица 2
Сообщение Решение. На вход кодера поступает одно из сообщений По формуле (4.19) [1] взаимная информация, содержащаяся в первом кодовом символе 1 относительно сообщения
Обратная вероятность
где т.е. условная вероятность Итак,
а взаимная информация, содержащаяся в первом кодовом символе 1 относительно сообщения
Информация, содержащаяся во втором кодовом символе 0 при условии, что первый кодовый символ был 1, есть
Информация, содержащаяся в третьем кодовом символе 1 при условии, что ему предшествовали 10, есть
Так как сообщения
Действительно,
Вычислить взаимные информации Решение. Дискретный канал с шумом удобно изображать в виде графа (рис. 3). Определим взаимную информацию по формуле (4.19) [1]
или в силу свойства симметрии
Условные и безусловные вероятности найдем, воспользовавшись таблицей. По формуле (1.7) [1]
Используя формулы (1.9), (1.10) [1], найдем условные вероятности:
Тогда количество взаимной информации по формуле (4.19) [1]
Мы получили Пример 8. Производится стрельба по двум мишеням, по одной сделано 2 выстрела, по второй – 3. Вероятности попадания при одном выстреле соответственно равны 1/2 и 1/3. Исход стрельбы (число попаданий) по какой мишени является более определенным? Решение. Исход стрельбы определяется числом попаданий в мишень, которое подчинено биномиальному закону распределения
Мерой неопределенности исхода стрельбы служит энтропия числа попаданий. Энтропия числа попаданий при стрельбе по первой мишени (4.6) [1]
Аналогично для второй мишени имеем
т.е. исход стрельбы по второй мишени обладает большей неопределенностью. Пример 9. Источник сообщений вырабатывает ансамбль символов
Символы в последовательности независимы. Вычислить энтропию источника и определить избыточность. Решение. Энтропия источника для случая неравновероятных и независимых сообщений определяется формулой (4.6) [1]
Избыточность за счет неоптимальности (неравновероятности) распределения сообщений в источнике определяется формулой (4.12) [1] Отсюда Пример 10. Алфавит источника состоит из трех букв: Определить энтропию на 1 букву текста а) буквы алфавита неравновероятны:
в) символы в последовательности независимы, вероятности букв одинаковы. Вычислить избыточность источников для случаев а) и б). Решение. а) В случае неравновероятных и зависимых сообщений энтропия текста по формуле (4.10) [1]
где а условная энтропия равна
Энтропия на один символ
б) При неравновероятных, но зависимых сообщениях энтропия вычисляется по формуле (4.6) [1]
Избыточность, обусловленная статистической зависимостью
в) В случае равновероятных и независимых сообщений энтропия по формуле (4.7) [1]
Избыточность, обусловленная неоптимальностью распределения вероятности
Полная избыточность (за счет неоптимальности распределения и наличия статистических взаимосвязей)
Пример 11. Вычислить для конкретного канала, заданного в примере 7, средние количества информации.
Решение. а) Средняя взаимная информация в реализации сигнала на выходе y 1 относительно случайной величины X на входе канала определяется формулой
Из примера 7 известны вероятности:
Определим условные вероятности:
Средняя информация
б) Средняя взаимная информация в выходной величине Y относительно реализации случайной величины на входе x 1 определяется формулой
Определяем условные вероятности
Условная средняя взаимная информация равна
в) Средняя взаимная информация между случайной величиной Y на выходе канала и случайной величиной X на входе определяется формулой (4.23) [1]
Воспользовавшись результатами вычислений
Пример 12. Эргодический источник имеет алфавит, состоящий из 8 букв. Средние частоты повторения букв одинаковы. При передаче по каналу с шумом в среднем половина всех букв принимается правильно, в другой половине случаев имеют место ошибки, при этом любая буква переходит в любую другую с одинаковой вероятностью. Какова средняя информация в принятой букве относительно переданной? Решение. Обозначим
ансамбль переданных букв,
ансамбль принятых букв. Так как для эргодической последовательности средние по времени частоты повторения букв совпадают с вероятностями, то по условию задачи вероятности появления букв на входе канала Ищем условные вероятности Другая половина случаев есть ошибочный прием, причем по условию задачи все возможные ошибки равновероятны. Числовозможных переходов (ошибок) равно 7. Тогда вероятность ошибки
Этот же результат следует непосредственно из того факта, что рассматриваемый канал – симметричный (набор вероятностей ошибок одинаков для любого Х), тогда при равномерном распределении на входе распределение на выходе также равномерно. Среднюю взаимную информацию находим по формуле (4.23) [1]
Выражения в квадратных скобках
Пример 13. Сообщение X есть стационарная последовательность независимых символов, имеющих ряд распределения
Определить: а) средние безусловную и условную энтропии, приходящиеся на 1 символ сообщения; б) средние безусловную и условную энтропии, приходящиеся на 1 символ сигнала; в) среднюю взаимную информацию в расчете на 1 символ сообщения. Решение. Символы в последовательности на выходе источника независимы, поэтому из (4.30) [1]
Обозначив y 1=00, у 2=1, вычислим условные и безусловные вероятности сигнала:
Энтропия случайной величины Y равна
а условная энтропия H(Y/X) =0, так как сигнал однозначно определяется сообщением. Взаимная информация
Условная энтропия сообщения
Итак, получаем, что условная энтропия сообщения равна 0, 2755 бит/симв, а взаимная информация в расчете на 1 символ сообщения равна 0, 8813 бит/симв. Среднее количество символов сигнала, приходящихся на 1 символ сообщения, равно
где lj – длина кодового слова, соответствующего xj. Энтропия последовательности Y(t) равна
а условная энтропия равна нулю. Пример 14. Вольтметром измеряется напряжение в электрической сети. Ошибка измерения не зависит от истинного значения напряжения и распределена нормально с нулевым математическим ожиданием и среднеквадратическим отклонением, равным 2 В. Истинное значение напряжения в сети также имеет нормальное распределение с математическим ожиданием 220 В и СКО, равным 10 В. Найти: а) зависимость величины получаемой информации от показаний прибора, б) среднюю величину получаемой информации. Решение. Введем обозначения: X – напряжение в сети, V – ошибка измерения, Y = X + V – показание прибора. Из условия задачи записываем плотности вероятностей:
Безусловную плотность вероятности величины Y можно найти по формуле полной вероятности, но проще поступить следующим образом. Показание прибора Y есть сумма двух независимых нормальных случайных величия и, следовательно, Y также имеет нормальное распределение с математическим ожиданием
и дисперсией
Итак,
Условную плотность вероятности х находим по формуле Байеса
В выражении, стоящем под знаком экспоненты, осуществляем возведение в квадрат и затем группируем члены, содержащие х 2 и х. В итоге убеждаемся, что условное распределение величины х также нормально
где ожидание X,
Для ответа на вопрос п. а) следует по формуле (3.1.2) вычислить величину средней взаимной информации между ансамблем X и реализацией у
Находим квадраты разностей и выносим за знак математического ожидания слагаемые и множители, не зависящие от х. Далее учитываем, что вычисляются условные математические ожидания при конкретном значении у, поэтому
В итоге получаем
Таким образом, искомая зависимость есть параболическая функция разности Для ответа на вопрос п. б) необходимо найти среднюю величину взаимной информации между ансамблями X и Y. Вычисляем безусловное математическое ожидание величины I (Х; у). При этом учитываем, что
Обратите внимание, что в среднем количество получаемой информации в данном примере зависит только от отношения «сигнал/ошибка» Пример 15. Положительная непрерывная случайная величина X распределена по экспоненциальному закону с математическим ожиданием mх =3. Вычислить значение дифференциальной энтропии величины X. Решение. Заданный закон распределения имеет вид
Дифференциальная энтропия непрерывной случайной величины X определяется формулой (4.40) [1]
Подставляя mx = 3, получим
|

 - сообщение о том, что объект находится в 46-м квадрате экрана.
- сообщение о том, что объект находится в 46-м квадрате экрана. . Безусловная вероятность сообщения – объект находится в 46-квадрате экрана – равна
. Безусловная вероятность сообщения – объект находится в 46-квадрате экрана – равна 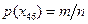 , где
, где  – общее число возможных исходов (квадратов поля),
– общее число возможных исходов (квадратов поля), 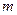 – число исходов, благоприятствующих событию
– число исходов, благоприятствующих событию  квадратов, a
квадратов, a  . Тогда
. Тогда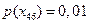 и
и 
 – объект находится в 5-й горизонтальной строке экрана – по аналогии с рассмотренным случаем а) определится
– объект находится в 5-й горизонтальной строке экрана – по аналогии с рассмотренным случаем а) определится  и собственная информация
и собственная информация
 – объект находится в 6-м вертикальном столбце и 3-й горизонтальной строке – равна
– объект находится в 6-м вертикальном столбце и 3-й горизонтальной строке – равна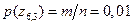 , следовательно,
, следовательно,
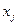
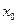





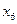

 .
.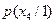 может быть найдена по формуле Байеса (1.9) [1]
может быть найдена по формуле Байеса (1.9) [1] ,
,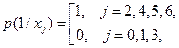
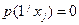 для гипотез, при которых первый кодовый символ есть 0, и
для гипотез, при которых первый кодовый символ есть 0, и  для гипотез, при которых первый кодовый символ 1. В знаменателе формулы Байеса таким образом учитываются те гипотезы, при которых возможно появление 1 на первом месте.
для гипотез, при которых первый кодовый символ 1. В знаменателе формулы Байеса таким образом учитываются те гипотезы, при которых возможно появление 1 на первом месте. ,
, ,
,  ,
,


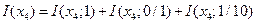 .
.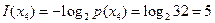 бит, и это совпадает с приведенной суммой.
бит, и это совпадает с приведенной суммой. Пример 7. По дискретному каналу передаются сообщения
Пример 7. По дискретному каналу передаются сообщения 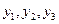 . Вероятности совместного появления
. Вероятности совместного появления  заданы табл. 3.
заданы табл. 3. ,
,  .
.

 .
. ;
; ;
;  ;
; ;
;  .
. ,
, .
.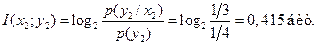

 , так как
, так как 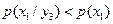 .
.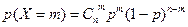 ,
, где
где 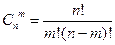 .
. Составляем ряд распределения для числа попаданий в первую мишень при n =2 и p =1/2 (табл. 4) и вторую мишень при n =3 и p =1/3 (табл. 5).
Составляем ряд распределения для числа попаданий в первую мишень при n =2 и p =1/2 (табл. 4) и вторую мишень при n =3 и p =1/3 (табл. 5).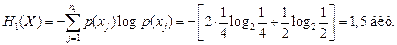

 .
.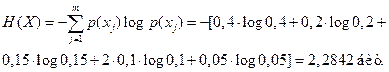
 , где
, где  по формуле (2.2.3).
по формуле (2.2.3).
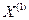 ,
,  для следующих случаев:
для следующих случаев: ,
,  , а символы в последовательности на выходе источника статистически зависимы. Условные вероятности
, а символы в последовательности на выходе источника статистически зависимы. Условные вероятности  заданы в табл. 6;
заданы в табл. 6; б) вероятности букв те же, что и в п. а), но символы независимы;
б) вероятности букв те же, что и в п. а), но символы независимы; ,
, ,
,



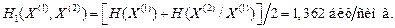

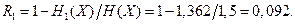



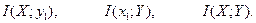



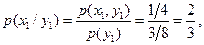


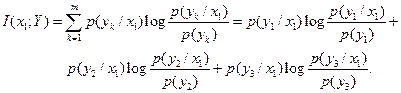
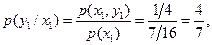
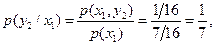

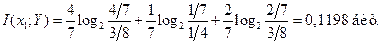
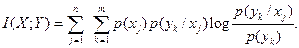
 , получим для средней взаимной информации
, получим для средней взаимной информации



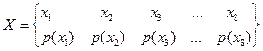 –
–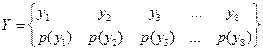 –
–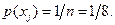
 . Поскольку половина всех букв принимается правильно, то
. Поскольку половина всех букв принимается правильно, то 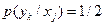 при
при 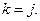
 при
при 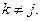

 Вероятности появления букв на выходе найдем по (1.7) [1]
Вероятности появления букв на выходе найдем по (1.7) [1] для любого к.
для любого к.


 численно равны, поэтому
численно равны, поэтому

 Сигнал Y является последовательностью двоичных символов, связанных с сообщением следующим неудачным образом: x1→ 00, x2→ 00, x3→ 1.
Сигнал Y является последовательностью двоичных символов, связанных с сообщением следующим неудачным образом: x1→ 00, x2→ 00, x3→ 1.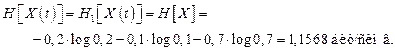


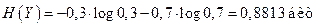 ,
,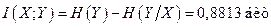 .
. .
.




 .
.
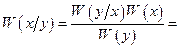
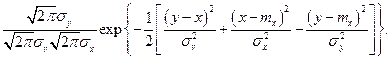
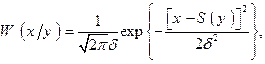
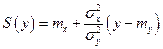 – условное математическое
– условное математическое - условная дисперсия X.
- условная дисперсия X.


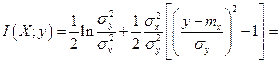


 , причем наименьшее количество информации, равное 1, 1482 нат, доставляет наиболее вероятное показание прибора
, причем наименьшее количество информации, равное 1, 1482 нат, доставляет наиболее вероятное показание прибора 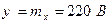 .
.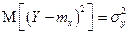 , и получаем
, и получаем




 .
.


