Кодирование
Решение. В соответствии с алгоритмом построения кода Хафмана делаем последовательно следующие шаги: 1) располагаем сообщения источника в порядке убывания вероятностей; 2) образуем вспомогательный алфавит, объединяя наиболее маловероятные буквы u 1 и u 4 (m 0=2), тогда вероятность новой буквы равна p 1= р (u 1)+ р (u 4)=0, 1+0, 05=0, 15. Оставляем эту букву на месте, так как p 1= р (u 6); 3) объединяем первую вспомогательную букву и букву u 6, тогда вероятность второй вспомогательной буквы равна р 2= р 1+ р (u 6)=0, 15+0, 15=0, 3; перемещаем ее вверх в соответствии с этой вероятностью; 4) объединение продолжаем до тех пор, пока в ансамбле не останется единственное сообщение с вероятностью единица.
Сообщения источника являются теперь концевыми узлами кодового дерева. Приписав концевым узлам значения символов 1 и 0, записываем кодовые обозначения, пользуясь следующим правилом: чтобы получить кодовое слово, соответствующее сообщению u 4, проследим переход u 4 в группировку с наибольшей вероятностью, кодовые символы записываем справа налево (от младшего разряда к старшему), получим 1100. Для сообщения u 1 – 1101 и т.д. (см. рис. 4). Оценим эффективность полученного кода. Энтропия источника сообщений:
на одну букву на выходе источника. Средняя длина кодового слова (формула (4.14) [1])
Для оценки эффективности кода используем коэффициент эффективности Для оптимального двоичного кода Полученный нами код имеет Пример 17. Сообщение источника X составляется из статистически независимых букв, извлекаемых из алфавита А, В, С с вероятностями 0, 7; 0, 2; 0, 1. Произвести двоичное кодирование по методу Шеннона-Фано отдельных букв и двухбуквенных блоков. Сравнить коды по их эффективности. Решение. Производим побуквенное кодирование методом Шеннона-Фано. 1) Располагаем буквы алфавита источника в порядке убывания вероятностей. 2) Делим алфавит источника на две (m =2) примерно равновероятные группы. Всем сообщениям верхней группы (буква А) приписываем в качестве первого кодового символа 1, всем сообщениям нижней группы приписываем символ 0.
Оценим эффективность полученного кода. Энтропия источника
Средняя длина кодового слова
Видим, что L > H (X), и коэффициент эффективности
При блоковом кодировании средняя длина кодового слова на одну букву
При этом коэффициент эффективности
Избыточность при двухбуквенном кодировании R 2=0, 0045. Получили γ 2 > γ 1, R 2< < R 1, что и требовалось показать. Пример 18. Способ кодирования задан кодовой таблицей
б) найти кодовое расстояние; в) определить кратности обнаруживаемых и исправляемых ошибок; г) определить избыточность кода, полагая буквы источника равновероятными. Решение. а) Матрицу расстояний записываем в виде таблицы (табл. 10).
в) Кратность обнаруживаемых ошибок определяется по формуле (3.5) [1], откуда q о≤ 3. Кратность исправляемых ошибок находим по формуле (3.6) [1] q и≤ 1, 5. Следовательно, приведенный код позволяет обнаруживать всевозможные однократные, двукратные и трехкратные ошибки и исправлять любые однократные ошибки. г) Избыточность кода находим из следующих соображений. Для передачи равновероятных сигналов a1, а2, а3, а4 достаточно передавать кодовые слова 00, 10, 01 и 11 соответственно. Такой код не имеет избыточности, но не позволяет обнаруживать и, тем более, исправлять ошибки. Для обнаружения и исправления ошибок введены пять избыточных символов, т.е. количественно избыточность равна Пример 19. Линейный блочный (5, 2)-код задан производящей матрицей G в систематической (канонической) форме
Произвести декодирование следующими методами: а) по минимуму расстояния; б) вычислением синдрома. Решение. Если производящая матрица записана в каноническом виде, это значит, что она состоит из двух блоков: диагональной матрицы размера k Проверочная матрица Н также может быть записана в каноническом виде и состоит из двух блоков. Первый блок есть прямоугольная матрица размера k Для заданного кода получаем
Убедимся, что полученная таким образом матрица Н удовлетворяет соотношению (3.18) [1]. Действительно,
т.е. все 6 элементов матрицы GHT равны нулю. Построим кодовую таблицу, воспользовавшись правилом образования кодовых слов по формуле (3.21) [1]: a1 =00000, а2 =10110, а3 =01011, а4 = 11101= a2 + a3. Всего кодовая таблица содержит 2 k = 4 вектора. Из кодовой таблицы определяем величину кодового расстояния Следовательно, рассматриваемый код обнаруживает однократные и двукратные ошибки и исправляет однократные. Декодируем принятый вектор b = 00110.
По величине dib min =1 решаем, что передавался вектор а2 =10110, следовательно, ошибка в первом символе кодового слова, а информационная последовательность имеет вид х = 10. б) Метод декодирования с помощью вычисления синдрома включает следующие операции: 1) По формуле (3.17) [1] заранее устанавливаем однозначную связь между векторами однократных ошибок е и соответствующими им синдромами. Все возможные векторы
c1=(00110)(10100)=1, с2=(00110)(11010)=1, с3=(00110)(01001)=0, т.е. вектор с = 110. Синдром не равен нулю, следовательно, есть ошибка. Вектору с = 110 в табл. 12 соответствует вектор ошибки в первом символе е =10000. Декодируем, суммируя принятый вектор с вектором ошибки Итак, получили тот же результат: передавался вектор a2 =10110, соответствующий информационной последовательности х =10. Пример 20. Для кода, заданного в примере 19, составить схему кодирующего устройства. Решение. Обозначим буквами а 1,..., а 5 символы на выходе кодера, причем а 1 и а 2 есть информационные символы, поступающие на его вход, а символы а 3, а 4 и а 5 образуются в кодере. Из соотношения (3.22) [1] получаем
Один из вариантов схемы кодера, определяемой этими соотношениями, показан на рис. 5. Кодирующее устройство работает следующим образом. В течение первых двух шагов двухразрядный регистр сдвига заполняется информационными символами а 1 и а 2, а в течение Пример 21. Построить код Хэмминга, имеющий параметры: dкод =3, r =3. Решение. Построение кода начинаем с проверочной матрицы. В качестве семи столбцов проверочной матрицы Н выбираем всевозможные 3-разрядные двоичные числа, исключая число нуль. Проверочная матрица имеет вид
Чтобы определить места проверочных и информационных символов, матрицу Н представляем в каноническом виде
Для этого достаточно в матрице Н выбрать столбцы, содержащие по одной единице, и перенести их в правую часть. Тогда получим
Из формулы (4.3.5) получаем следующие соотношения для символов a 1,..., а 7 кодового слова:
Пользуясь этими соотношениями, составляем кодовую таблицу
Пример 22. Для кода Хэмминга, определяемого проверочной матрицей H, построенного в примере 21, декодировать принятый вектор 1011001. Решение. Для принятого вектора b =1011001 по формуле (3.16) [1] вычисляем синдром
Синдром с ≠ 0, т.е. имеет место ошибка. В случае одиночной ошибки (и только лишь) вычисленное значение синдрома всегда совпадает с одним из столбцов матрицы Н, причем номер столбца указывает номер искаженного символа. Видим, что ошибка произошла в первом символе и передавался вектор Пример 23. Производится кодирование линейным блочным кодом (15, 15- r). Найти минимальное количество проверочных символов r, при котором код был бы способен исправлять любые однократные, двукратные и трехкратные ошибки. Решение. Поскольку в кодовой комбинации n =15 символов, то количество всевозможных однократных ошибок (q =1) равно
Чтобы любая из этих ошибок могла быть исправлена, нужно, чтобы разным ошибкам соответствовали различные значения синдрома c. Вектор c состоит из r двоичных символов, тогда максимальное количество различных ненулевых комбинаций равно
Таким образом, для исправления всех упомянутых ошибок необходимо, чтобы передаваемые комбинации содержали не менее 10 проверочных символов, т.е. k =5. Пример 24. Для кодирования применяется (15, 5)-код БЧХ с кодовым расстоянием dкод =7, способный исправить все ошибки до трехкратных включительно. Битовая вероятность ошибки в канале передачи p =10-4, ошибки независимы. Определить вероятность ошибки при декодировании кодовой комбинации и битовую вероятность ошибки на выходе декодера. Решение. Вероятность ошибки при декодировании кодовой комбинации определим по формуле (3.59) [1]
Битовую вероятность ошибки на выходе декодера определим по формуле (3.60) [1]
|

 Пример 16. Закодировать сообщения источника, приведенные в табл 7, двоичным кодом Хафмана. Оценить эффективность полученного кода.
Пример 16. Закодировать сообщения источника, приведенные в табл 7, двоичным кодом Хафмана. Оценить эффективность полученного кода. Построение кода Хафмана приведено на рис. 4.
Построение кода Хафмана приведено на рис. 4.


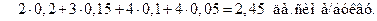 .
.
 и
и  .
. избыточность R =0, 0109, т.е. код близок к оптимальному.
избыточность R =0, 0109, т.е. код близок к оптимальному. 3) Производим второе разбиение на две группы (буквы В и С) и снова букве в верхней группе (В) приписываем символ 1, а в нижней (С) в качестве второго символа кодового слова приписываем 0. Так как в каждой группе оказалось по одной букве, кодирование заканчиваем. Результат приведен в табл. 8.
3) Производим второе разбиение на две группы (буквы В и С) и снова букве в верхней группе (В) приписываем символ 1, а в нижней (С) в качестве второго символа кодового слова приписываем 0. Так как в каждой группе оказалось по одной букве, кодирование заканчиваем. Результат приведен в табл. 8.

 .
. а избыточность R 1=0, 1102.
а избыточность R 1=0, 1102. Покажем, что кодирование блоками по 2 буквы (k =2) увеличивает эффективность кода. Строим вспомогательный алфавит из N =32 блоков. Вероятности блоков находим по формуле (1.8) [1], считая буквы исходного алфавита независимыми. Располагаем блоки в порядке убывания вероятностей и осуществляем кодирование методом Шеннона-Фано. Все полученные двухбуквенные блоки, вероятности их и соответствующие кодовые обозначения сведены в табл. 9.
Покажем, что кодирование блоками по 2 буквы (k =2) увеличивает эффективность кода. Строим вспомогательный алфавит из N =32 блоков. Вероятности блоков находим по формуле (1.8) [1], считая буквы исходного алфавита независимыми. Располагаем блоки в порядке убывания вероятностей и осуществляем кодирование методом Шеннона-Фано. Все полученные двухбуквенные блоки, вероятности их и соответствующие кодовые обозначения сведены в табл. 9.
 .
.
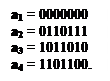 a) составить матрицу расстояний
a) составить матрицу расстояний 
 ;
; б) По табл. 10 находим кодовое расстояние
б) По табл. 10 находим кодовое расстояние 
 .
. Пусть принят вектор b =00110 и известно, что возможны только одиночные ошибки.
Пусть принят вектор b =00110 и известно, что возможны только одиночные ошибки. k, состоящей из единиц, и прямоугольной матрицы размера r
k, состоящей из единиц, и прямоугольной матрицы размера r  .
.
 .
. а) Метод декодирования по минимуму расстояния заключается в том, что, вычислив расстояния вектора b относительно всех векторов аi кодовой таблицы, отождествляем принятый вектор с тем, расстояние до которого минимально. Расстояния dib приведены в табл. 11.
а) Метод декодирования по минимуму расстояния заключается в том, что, вычислив расстояния вектора b относительно всех векторов аi кодовой таблицы, отождествляем принятый вектор с тем, расстояние до которого минимально. Расстояния dib приведены в табл. 11. приведены в табл. 12.
приведены в табл. 12. 2) Вычисляем синдром для принятого слова b по формуле (3.16) [1] с = bHT:
2) Вычисляем синдром для принятого слова b по формуле (3.16) [1] с = bHT:

 следующих трех тактов его состояние сохраняется неизменным. Одновременно с заполнением регистра начинается переключение мультиплексора (переключателя) MUX. Таким образом формируются 5 символов кодового слова, удовлетворяющих требуемым соотношениям.
следующих трех тактов его состояние сохраняется неизменным. Одновременно с заполнением регистра начинается переключение мультиплексора (переключателя) MUX. Таким образом формируются 5 символов кодового слова, удовлетворяющих требуемым соотношениям.
 где I – единичная матрица.
где I – единичная матрица.




 Количество различных двукратных и трехкратных ошибок равно числу сочетаний
Количество различных двукратных и трехкратных ошибок равно числу сочетаний  и
и  соответственно. Тогда суммарное количество всевозможных ошибок при q ≤ 3 равно
соответственно. Тогда суммарное количество всевозможных ошибок при q ≤ 3 равно
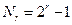 (нулевая комбинация c=0 соответствует отсутствию ошибок). Отсюда получаем
(нулевая комбинация c=0 соответствует отсутствию ошибок). Отсюда получаем  (это ограничение называется пределом Хэмминга), то есть
(это ограничение называется пределом Хэмминга), то есть


 то есть, одна ошибка приходится в среднем на
то есть, одна ошибка приходится в среднем на  бит.
бит.


