Другие меры информации
Пример 25. Случайная величина H1: m = m 1, H2: m = m 2. Решение. Запишем плотности вероятности случайной величины
По формуле (4.43) [1] находим информацию для различения в пользу Н1 против Н2, содержащуюся в выборочном значении
По формуле (4.44) [1] находим среднюю информацию для различения в пользу Н1 против Н2
Далее учтем, что при гипотезе Н1 математическое ожидание
По формулам (4.45) и (4.46) [1] находим
Таким образом, средняя информация для различения гипотез Н1, и Н2 в данной задаче пропорциональна квадрату расстояния между математическими ожиданиями сигнала Пример 26. Случайная величина Y имеет экспоненциальное распределение
а) Найти максимально правдоподобную оценку математического ожидания m этой случайной величины. б) Найти статистические характеристики (математическое ожидание и дисперсию) этой оценки. д) Найти информацию Фишера и по неравенству Рао-Крамера проверить сделанное заключение об эффективности оценки. Решение. Запишем уравнение правдоподобия
Отсюда Далее находим математическое ожидание оценки
Таким образом, оценка Дисперсию оценки вычисляем по
Информацию Фишера находим по формуле (4.48) [1]
Видим, что неравенство Рао-Крамера (4.49) [1] обращается в равенство, следовательно, оценка эффективна. Лучшей оценки, т.е. обладающей меньшей дисперсией при отсутствии систематической ошибки, не существует.
|

 имеет нормальное распределение с известным среднеквадратическим отклонением
имеет нормальное распределение с известным среднеквадратическим отклонением  . Вычислить I (1: 2), I (2: 1), J (1, 2) для следующих гипотез о математическом ожидании этой величины:
. Вычислить I (1: 2), I (2: 1), J (1, 2) для следующих гипотез о математическом ожидании этой величины: ,
, .
.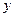 (в этой задаче удобнее использовать натуральные единицы информации):
(в этой задаче удобнее использовать натуральные единицы информации):



 , и получим окончательно
, и получим окончательно .
.
 .
. .
.
 , т.е. максимально правдоподобная оценка математического ожидания равна наблюдаемому выборочному значению
, т.е. максимально правдоподобная оценка математического ожидания равна наблюдаемому выборочному значению  .
. является несмещенной.
является несмещенной. .
.



