Метод оценки точности обработки заготовок с помощью кривых распределениях
Случайные погрешности и законы их распределения изучаются в теории вероятности и математической статистики. Для оценки точности размеров обработанных заготовок используют метод кривых распределения. Метод кривых распределения и больших выборок позволяет объективно оценить точность при больших выборах. В технологии машиностроения встречаются законы распределения случайных величин: Гаусса, Симпсона, Релея и другие. При обработке на настроенных станках очень часто рассеяние размеров заготовок подчиняется закону нормального распределения (закону Гаусса) (рис. 1.18). Средний размер заготовки по чертежу равен среднему арифметическому значению предельных размеров детали (1.46).
где D max и D min – наибольший и наименьший предельный размеры детали на чертеже. Рассеяние размеров в партии деталей рассчитывается по формуле (1.47):
где D нб – наибольший размер, в партии заготовок; D нм – наименьший размер в партии заготовок; σ – среднее квадратичное отклонение размера деталей (1.48).
где
Если рассеяние превышает величину допуска ω > Т, то появляется брак. Для наружных размеров площадь А характеризует неисправимый брак, а площадь Б исправимый (рис. 1.18).
Рис. 1.18. Схема определения случайной погрешности обработки
Общая площадь под кривой ограниченная 6σ характеризует вероятность попадания 99, 73% из 100% всех размеров партии деталей. За случайную погрешность Dcл принимается величина рассеяния размеров в партии деталей (1.50). Dcл = 6σ (1.50)
|
, (1.46)
, (1.47)
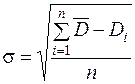, (1.48)
– среднее арифметическое значение размеров партии деталей (1.49).
. (1.49)
