Statically indeterminate problems
Construction calculation problems in which elements of the force factors cannot be determined by the equations of the static’s balance alone are called statically indeterminate. To solve such problems apart from balance equations displacement and deformation equations are made. The details temperature change causes their dimensions change and as a result additional stresses called temperature stresses arise in the statically indeterminate systems. Let us consider a weightless bar of the constant section of the A area and the
from then we get that the Rc and Rв reactions are equal. Having applied the section method we establish that the N normal force at the bar section is equal to the unknown reactions:
Compose an additional equation removing the damped right mentally and replacing it by the RB reaction. The additional equation will be as follows
(i.e. the bar temperature elongation is equal to its shortening under the Rc reaction action, because the constraints are absolutely rigid).
Fig. 2.4.
The temperature elongation
Let us determine the temperature stresses:
To avoid the temperature stresses achieving considerable values, one of the bridge’s send is put on the rollers. The compensator systems are made in the long pipelines that are subjected to the temperature changes. Example. An absolutely ridid bar pictured in Fig.2.5 is pin-connected to the wall and hung up on two pinned and vertically placed steel bars that have the same length L = 2m. The force F = 20 kN acts at the D point of the bar. The cross section areas are the same: А1 = 3 сm2, A2 = 6 сm2. The material elasticity modulus for the bars is Е = 2.105 МPа, the weight force of the bar is G = 40 kN. Determine the stresses for the bars 1 and 2.
Fig. 2.5.
Solution. Considering the bar equilibrium, having removed the constraints and replacing them by their reactions, we get three unknowns: the Ra reaction of the A pin and the Rc and Rв reactions of the bars 1 and 2. For the given parallel forces system only two equilibrium equations can be composed: the forces projection equation for the vertical axis and the moments equation relative to any point; hence, we have a statically indeterminate system. To solve the problem it is necessary to compose an additional displacement equation for the construction elements. Imagine it in the deformed form. From the triangle resemblance ACC’ and ABB’ we receive
hence it follows
Compose the moments equation relative to the point A:
Simplifying the last equation, we get
4Rс + 10Rв = 5G + 7F.
According to Hooke’s law
Divide the second equation by the first one:
As Determine Rв and Rc: 4Rc+50Rc = 5G+7F, 54Rc = 5 . 40 +7 . 20 = 340. So, Rс= 340/54=6, 3 кN and RB= 5Rc= 5 . 6, 3 = 31, 5 кN.
Determine
|

 length with rigidly clamped ends (Fig. 2.4). The tension temperature stresses arise in the bar under heating. Let us determine these stresses. Compose the equilibrium equation for the bar:
length with rigidly clamped ends (Fig. 2.4). The tension temperature stresses arise in the bar under heating. Let us determine these stresses. Compose the equilibrium equation for the bar:


 , where α is the bar coefficient of linear expansion; the shortening under the Rc reaction action is
, where α is the bar coefficient of linear expansion; the shortening under the Rc reaction action is  Equate the right parts of these equalities:
Equate the right parts of these equalities: hence
hence 




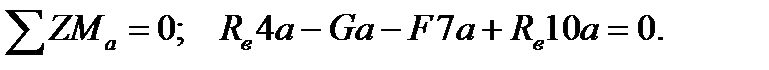


 , and А2 =2А1, then
, and А2 =2А1, then  , hence
, hence 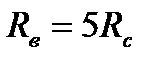 .
. and
and  stresses for the bars:
stresses for the bars:



