Determination of stresses at the inclined sections in tension (compression) in two directions
Let us consider a general case of the plane stress state, when two principal stresses ( The indices for denoting the principal stresses are put so as the The angle between the The
wherefrom
further,
wherefrom
From the formula (2.9) it is evident that the maximum shearing stresses are equal to half the difference of the principal stresses:
Special cases. The first case. Let us consider the stress state, under which In this case for all sections passing through the point under study the shearing stress The second case. Let us consider the stress state as presented in Fig. 2.7 d, characterized by the principal stresses Determine the stresses at the sections having the same slope to the directions We get
|
in Fig. 2.7 a) differ from zero.
inequality is observed. We shall count off the positive 
angle between the 
direction and the normal to the arbitrary section against the clock.
stress direction and the plane is equal to 
and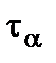 
stresses at the arbitrary inclined section can be determined from the equilibrium condition of the ABC trihedral prism (Fig. 2.7 b) or calculated by the formulae (2.3) and (2.4) by summing the stresses caused by 
and the stresses caused by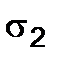 
. As a result we get
(2.8)
(2.9)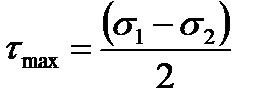
. (2.10)
(Fig. 2.7 c).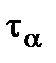
is equal to zero, and the normal stress has the same value 
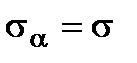. That kind of the stress state is called the uniform plane tension (or compression).
and 
. Then, 
.
and 
i.e. at 
= 45° and 
= 135°.
; 
by the formulae (2.8) and (2.9). This stress state is called the pure shear.
