First moment of an area
Under some deformations the details strength depends not only on the cross section area but also on its shape. Up to now we studied the deformations which have the stresses depending on the cross section area. To study the deformation of torsion and bending we have to know some other geometric figures plane characteristics. The first moment of the plane figure about any axis in the plane of the area is given by summation of the elemental areas products and the perpendicular distances between the element and the axis (Fig. 3.1). Denote by S the first moment of the area with the corresponding axis index:
Fig. 3.1.
The formulas to determine the centroidal coordinates of the figure area are as follows:
Since in these formulas (3.2) by A we can mean dA elemental area, then the expressions of the numerators in the right parts of the formula are the first moment of a figure about the y and x – axes, and
The unit of the first moment of the figure area is the unit of the length. The first moment of the figure area can be a positive, negative and equal to zero value. Evidently, the first moment of the area about the axis passing through the centroid of the figure area (the central axis) and among the symmetry figure axis is equal to zero. In the formulas to determine the centroidal coordinate we can imply by the A area the finite figure parts, by x and y – the coordinates of these centroidal parts (i.e. to apply the division method). Hence, to determine the first moment of the area of a compound figure we can also apply the division method, i.e. to determine the first moment of all the figure as an algebraic sum of the first moments of its separate parts:
where Si is the first moment of each figure part area.
|

 (3.1)
(3.1)
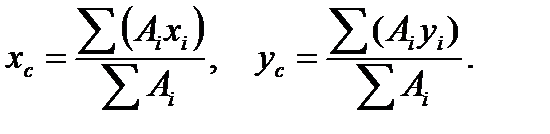 (3.2)
(3.2)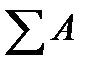 is the A area of the all figure. Consequently,
is the A area of the all figure. Consequently,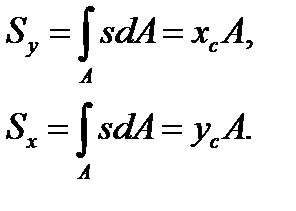 (3.3)
(3.3)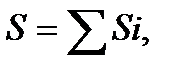 (3.4)
(3.4)


