The moment of inertia at parallel displacement of axis
The axes passing through the figure centroid are called central. The inertia moment about the central axis is called the central moment of inertia. The moment of inertia of an area is equal to the moment of inertia about a parallel axis through the centroid of the area plus the product of the area and square of the distance between the axes. Let us take an arbitrary plane figure having the area A, the centroid at the point С and the moment of inertia through the x axis is Ix. Determine the inertia moment of the figure about the
The first item on the right part is the inertia moment of the figure about x axis i.e. Ix; the second item contains the first moment of the area about x axis and it is equal to zero, because x axis is central; the third item is equal to а2А. Thus, we get
One should keep in mind the fact that we can use the last formula only when one of parallel axes is central. Analyzing the derived formula we can do the conclusion that the moment of inertia of the number of parallel axes will be the minimum one about the centroid axis.
Fig. 3.4.
Derive the formula of the inertia moment calculation of a rectangular about х1 axis passing through its base:
|
axis which is parallel to the centroidal axes and located at the distance a (Fig. 3.4):
(3.12)
(3.13)
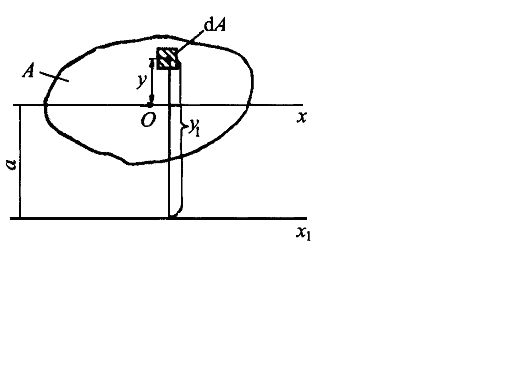
(3.14)
