As we can see the shearing strain and shearing stress in torsion are directly proportional to the distance from the centroid of the section
Fig. 4.6.
The shearing stress diagram over the bar cross section is shown as in Fig. 4.5 to the right. The shearing stresses are equal to zero at the centroid of the round section. The maximum shear stresses will be at the section points located on the bar surface. Knowing the distribution law of the shearing stresses we can easily determine them, the twisting moment at the section being the resultant moment of the shearing stresses at the section:
where Substituting the stresses value from the formula (4.3) in (4.4) we get
Bearing in mind that
where
Substituting the value
In this way the final formula for determining the shear stresses is
As it can be seen from this formula the stresses The maximum stresses are at the points of the section contour:
We call the sectional modulus of torsion or modulus of twist the geometrical characteristics Wp. The statically strength condition of the shaft is
here Besides the strength check by this formula we can find the shaft diameter or determine the allowable twisting moment when the other value is known. Keeping in mind that for the round solid section Wp = 0, 2d3 we get
The allowable twisting moment from the strength condition is determined by the formula
|


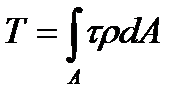 , (4.4)
, (4.4)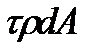 is the elemental twisting moment of the internal forces acting on the element of area dA.
is the elemental twisting moment of the internal forces acting on the element of area dA.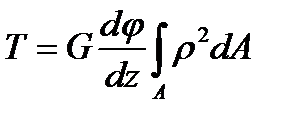 (4.5)
(4.5)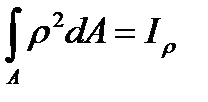 , (4.6)
, (4.6) is the polar moment of inertia of the section, we receive
is the polar moment of inertia of the section, we receive (4.7)
(4.7) in the formula (4.3) we have
in the formula (4.3) we have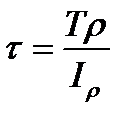 (4.8)
(4.8)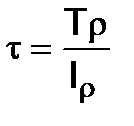 (4.9)
(4.9)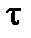 are the same at the points removed equally from the section center.
are the same at the points removed equally from the section center.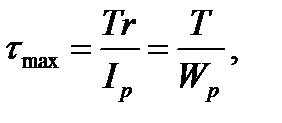 (4.10)
(4.10)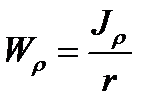 . (4.11)
. (4.11) , (4.12)
, (4.12)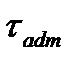 is the allowable working shear stress.
is the allowable working shear stress.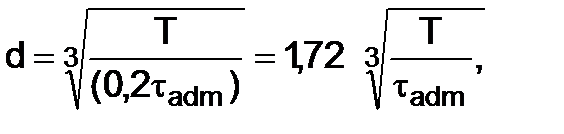 (4.13)
(4.13)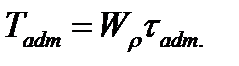 (4.14)
(4.14)


