Principal axes and principal moment of inertia
Let us imagine the plane figure that has the moment of inertia about the coordinate axes Ix and As it was determined earlier
The polar moment of inertia will be constant but the axial moments of inertia will change if we rotate the initial coordinates in its plane and what is more
If the sum of two variable values remains constant, one of them decreases but the other one increases. Hence, under some axis position one of the second moments reaches the maximum value and the other - the minimum one. The axes about which the inertia moments have both maximum and minimum values are called the principal axes of inertia. The moment of inertia about the principal axis is called the principal moment of inertia. If the principal axis passes throw the figure centroid, it is called the principal central axis and the moment of inertia about this axis is called the principal central moment of inertia. The following circumstance is extremely important: if the figure has the axis of symmetry, the axis will always be one of the principal central axis. Let us introduce another geometric characteristics of the plane section. The product of inertia of the plane figure is called the sum of the products of the area elements and the perpendicular distance between the elements and the axes taken over the figure area:
where x, y are the distances between the elemental area dA and x and y axes. The product of inertia may be positive, negative and in a special case zero. If the mutually perpendicular axes x and y or one of them are the axis of the symmetry, the product of inertia is equal to zero about these axes. The product of inertia makes part of the formulas to determine the position of the principal axes of asymmetrical sections.
|

 and the polar moment of inertia
and the polar moment of inertia  about the initial coordinates.
about the initial coordinates.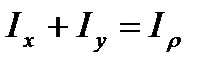
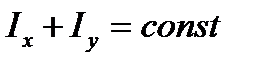 .
. , (3.15)
, (3.15)


