The practical formula for the stability analysis
It is comfortable to have one formula under any bar slenderness ratio then two formulas (Euler and Jasinsky) as each of them is good for a certain range of the slenderness ratio. This practical formula being applied widely in the construction design has the form
where The value
The allowable working stress has the form:
where The relation between the coefficient
from which
Using the formula (9.14) we get
To select the section the formula is led to the following form:
The value If we receive a large difference between the values
and so on as long as the difference between the successive values do not exceed 4-6%. For bars which sections have considerable weakness (for example, from holes) besides the stability design, the strength analysis must be done by the formula
where In the stability design the total section area Tabl. 9.1.
|

 (9.12)
(9.12) is the allowable working stress in compression;
is the allowable working stress in compression;  is the reduction coefficient for the allowable working stress (or a coefficient of buckling). The value
is the reduction coefficient for the allowable working stress (or a coefficient of buckling). The value  depends on the material and the slenderness ratio. Its values are given in tabl. 9.1; A is the bar cross section area.
depends on the material and the slenderness ratio. Its values are given in tabl. 9.1; A is the bar cross section area. can be considered as the allowable stress in the stability analysis, i.e.
can be considered as the allowable stress in the stability analysis, i.e. (9.13)
(9.13) (9.14)
(9.14) is the limit stress taken as the yield stress for plastic materials or the ultimate strength for the brittle ones.
is the limit stress taken as the yield stress for plastic materials or the ultimate strength for the brittle ones. the critical stress
the critical stress 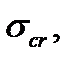 the limit stress
the limit stress  of the safety factor coefficients n and stability
of the safety factor coefficients n and stability  can be derived as follows:
can be derived as follows: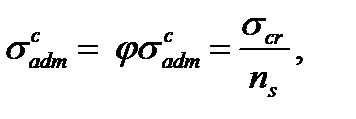
 (9.15)
(9.15) (9.16)
(9.16) (9.17)
(9.17) has to be set as the slenderness ratio
has to be set as the slenderness ratio  is unknown because the section area A is unknown but the slenderness ratio depends on it. Then one has to determine i min and λ values from tabl. 9.1 It is recommended to take φ 1 = 0.5. And then we find the values A, l min.
is unknown because the section area A is unknown but the slenderness ratio depends on it. Then one has to determine i min and λ values from tabl. 9.1 It is recommended to take φ 1 = 0.5. And then we find the values A, l min. and
and  , the calculation must be repeated setting a new value
, the calculation must be repeated setting a new value 
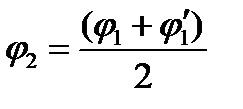
 (9.18)
(9.18) is the working area (net) of the bar section.
is the working area (net) of the bar section. is taken. In some cases (for example, in the machine-building construction element design) the values of the safety stability coefficients
is taken. In some cases (for example, in the machine-building construction element design) the values of the safety stability coefficients  provided for composing the tables of the coefficients
provided for composing the tables of the coefficients  are insufficient. In this case the design must be done by using the demanded coefficient
are insufficient. In this case the design must be done by using the demanded coefficient  and Euler’s or Jasinsky’s formula. It must be done the same in the design of the bar stability from materials which do not have coefficients in the table
and Euler’s or Jasinsky’s formula. It must be done the same in the design of the bar stability from materials which do not have coefficients in the table 

 for
for




