Calculating stresses under the uniformly accelerated motion
In many cases the acceleration with which the machine details displace is known. In this case the dynamic stresses are calculated without any difficulty. Consider some examples. Example 1. The load of the weight G is lifted up with the acceleration (Fig. 10.1). Determine the stress in the rope ignoring its weight.
Fig. 10.1. Fig. 10.2.
Solution. Apply to the load the force of inertia which is equal to Projecting all forces including the forces of inertia on the vertical axis we get
where Thus, in many cases the dynamic stress can be given by the static stress and the dynamic coefficient. It is very convenient as the dynamic coefficient must be often determined by an experimental way. Example 2. The bar of the weight q of the length 1 m is lifted by using two threads fastened to its ends (Fig. 10.2). The motion is translational at the acceleration a. Determine the stress in the bar. Solution. Apply to each element of the bar with the length equal to the unit the force of inertia The maximum bending moment will be at the section in the middle of the beam:
where The maximum dynamic stress is determined by the usual bend formula
|
directed down. Use the method of sections. Do the cut n-n and remove the upper rope part. Denote by 
the stress in the rope and as soon as the stresses in axial tension distribute uniformly over the section we can accept that 
where 
is the unknown dynamic stress in the rope.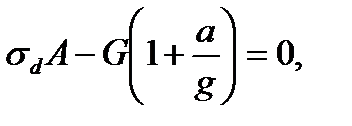
(10.1)
(10.2)
is the stress under the static load action; 
is the dynamic coefficient.
See, that this problem is equivalent to the problem of the simple beam loaded by the uniformly distributed load of the intensity 
(10.3)
is the bending moment from the static uniformly distributed load of the intensity q. 
- is the dynamic coefficient.
(10.4)
