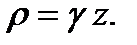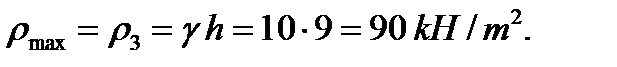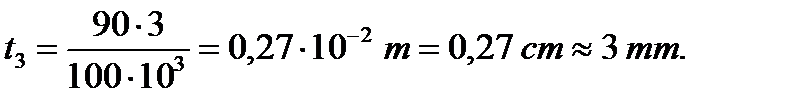Calculation of the thin-walled vessels
In technics there often occur the vessels whose walls are subject to pressure from liquids, gases and loose bodies (steam boilers, reservoirs, working chamber of motors, cisterns and the like). If the vessels have a shape of revolution bodies and their wall thickness is insignificant while the load is axisymmetric, the determining of stresses arising in their walls under the load is done very simply. In such cases, – it is not much of an error, it can be accepted that only normal stresses arise in the walls and that stresses are distributed over the wall thickness. The calculations based on such assumptions are well verified by the experiments if the wall thickness does not surpass approximately Remove from the vessel wall an element with the dimensions of
Рис. 8.1. Replace the interaction between the element and the remaining portion of the vessel by the internal forces having intensity Compose the element equilibrium condition by projecting the forces acting on the element in the direction of the normal nn to the element surface. The load projection is equal to Having projected all forces applied to the removed element on the normal direction nn we get
On account of a small element dimension this can be accepted.
Considering this from the equilibrium equation we get
Taking into account that
Reducing by
This formula is called Laplas’s formula. Consider the calculation of two vessel types often occurring in practice: spherical and cylindrical. Limit ourselves to the cases of the internal gas pressure action.
Fig. 8.2.
1. The spherical vessel. In this case we have
As in the given case the plane stress takes place, for the stress analysis it is necessary to apply this or that strength theory. The principal stresses have the following values:
i.e. checking the strength is realized as in the case of the uniaxial stress. According to the fourth strength hypothesis
i.e. the same condition and according to the third strength hypothesis. 2. The cylindrical vessel. In this case From Laplas’s equation we get
To determine the stress Projecting all forces on the vessel axis acting on the part cut we get
where Thus
Note that the ring area is calculated as the product of the circle length and the wall thickness because it is thin-walled and being the cylinder section over which there act the stresses
The strength condition according to the third strength hypothesis for the cylindrical vessel is
The strength condition according to the fourth strength hypothesis is
Example. Determine the wall thickness of the cylindrical vessel for saving the liquid with the specific weight g=10 kН/m3, the vessel dimentions shown in Fig. 8.3. The allowable working stress for the wall material is Solving. The liquid pressure on the wall vessel is proportional to the distance from the free surface:
Fig. 8.3.
If the wall thickness is constant the calculation then is made with the maximum pressure on the foundation:
The wall thickness is determined by the formula:
|

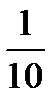 the minimum radius of the wall curvature.
the minimum radius of the wall curvature.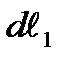 and
and 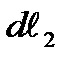 . Denote the wall thickness by t (Fig. 8.1). The radius of the curvature in this place is
. Denote the wall thickness by t (Fig. 8.1). The radius of the curvature in this place is 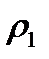 and
and 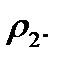 .The internal pressure
.The internal pressure 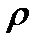 normal to the element surface is the load on the element.
normal to the element surface is the load on the element.
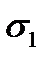 and
and 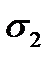 . As the wall thickness is insignificant, as it has been noted, these stresses can be considered as uniformly distributed over the wall thickness.
. As the wall thickness is insignificant, as it has been noted, these stresses can be considered as uniformly distributed over the wall thickness.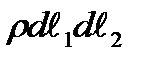 . The stress projection
. The stress projection  on the normal direction presents the segment ab which is equal to
on the normal direction presents the segment ab which is equal to 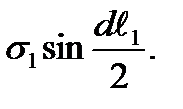 The stress projection acting on the border 1-4 (and 2-3) is equal to
The stress projection acting on the border 1-4 (and 2-3) is equal to 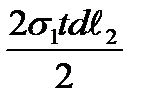 . Analogously, the stress projection acting on the border 1-2 (and 4-3) is equal to
. Analogously, the stress projection acting on the border 1-2 (and 4-3) is equal to 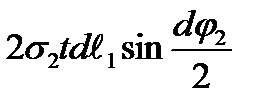 .
.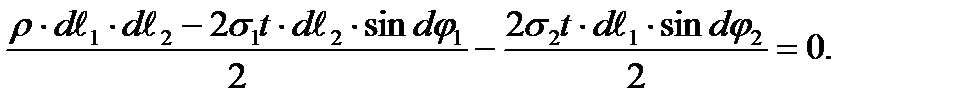
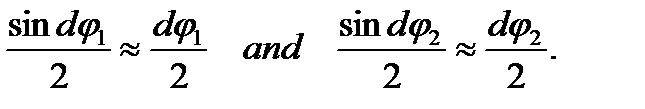

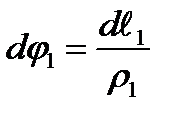 and
and 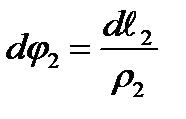 we have
we have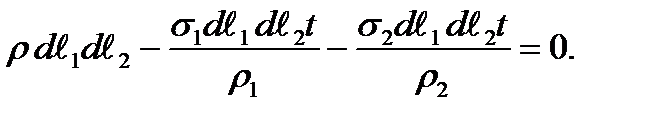
 and dividing by t we get
and dividing by t we get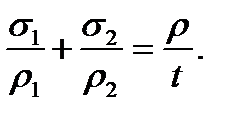 (8.1)
(8.1)
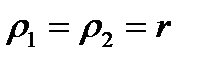 and
and 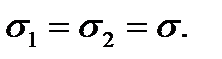 From (8.1) it follows that
From (8.1) it follows that 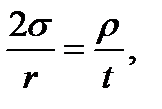 from which
from which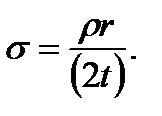 (8.2)
(8.2)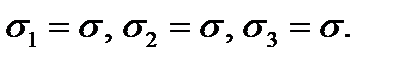 Under the third strength theory:
Under the third strength theory:  Substituting
Substituting 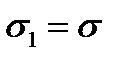 and
and 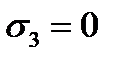 we get
we get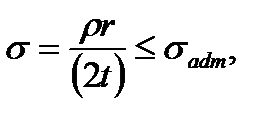 (8.3)
(8.3)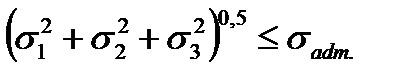 . As in the given case
. As in the given case 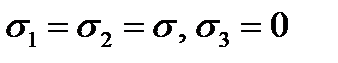 , we have
, we have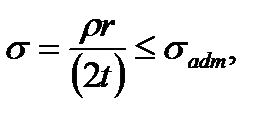 (8.4)
(8.4)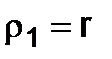 (the cylinder radius) and
(the cylinder radius) and 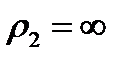 (the curvature radius of the forming line of the cylinder).
(the curvature radius of the forming line of the cylinder).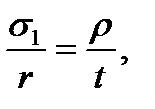 from which
from which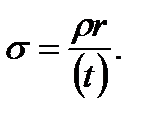 (8.5)
(8.5)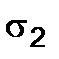 we cut the vessel by the plane perpendicular to its axis and consider the equilibrium condition of one of the vessel parts (Fig. 8.2 b).
we cut the vessel by the plane perpendicular to its axis and consider the equilibrium condition of one of the vessel parts (Fig. 8.2 b).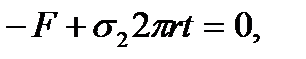 (8.6)
(8.6)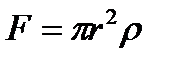 - the pressure force resultant of the gas on the vessel bottom.
- the pressure force resultant of the gas on the vessel bottom.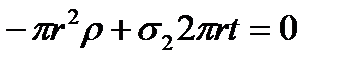 from which
from which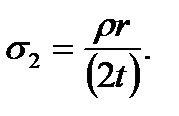 (8.7)
(8.7)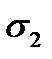 . Comparing
. Comparing 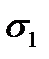 and
and 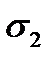 in the cylindrical vessel we see that
in the cylindrical vessel we see that
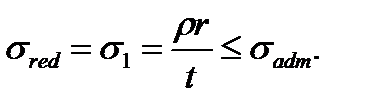 (8.8)
(8.8)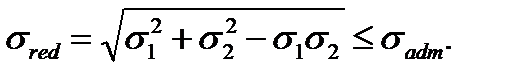 (8.9)
(8.9)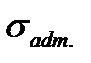 = 100 МPа =100.103 kPа.
= 100 МPа =100.103 kPа.