Создание онтологий
Процесс разработки онтологий во многом схож с развитием моделей сложных систем. Типичными являются следующие этапы создания конкретной онтологии. 1. Постановка задачи. На этом этапе изучается среда, для которой создается онтология, обдумывается, зачем нужна онтология, как и кем она будет использоваться. 2. Построение онтологии. Этот этап разбивается на три подэтапа: формализация понятий, кодирование и интеграция. В процессе формализации понятий осуществляется: а) выявление основных объектов и отношений предметной области (среды), б) текстовое описание этих объектов и отношений, в) сопоставление этим объектам термов, а отношениям – утверждений (аксиом). В процессе кодирования формируется описание на каком-либо формальном языке результатов предыдущего подэтапа. Обычно кодирование включает: а) выбор формального языка для кодирования, б) кодирование в выбранном языке термов и базовых отношений, в) описание с использованием введенных кодов термов и базовых отношений формул, соответствующих утверждениям. Подэтап интеграции выполняется параллельно двум упомянутым и требует тщательного обдумывания, каким образом вновь создаваемая онтология будет интегрироваться с уже существующими. 3. Формирование вопросов. На этом этапе осуществляются обдумывание и формальное описание вопросов, на которые онтология должна давать ответы, выбирается программная среда для реализации онтологии. Принципиальным для создания онтологии является не процедурный, а декларативный подход. Теоретической основой большинства языков, используемых для кодирования онтологий, являются различные исчисления, в основе которых, как правило, лежит логика предикатов первого порядка. Система теплоснабжения. В качестве конкретного примера создания онтологий рассмотрим ИИС проектирования зданий (интеллектуальную САПР), решающую важную задачу повышения эффективности систем теплоснабжения зданий. Основным материалом для проектирования реальных систем теплоснабжения зданий является архитектурный проект, который определяет размеры здания и его помещений, конструкции всех элементов здания, места установки и размеры окон и дверей, расположение инженерных сооружений, в частности систем теплоснабжения, канализации, вентиляции, т.е. всего, что необходимо в соответствии с действующими строительными нормами и правилами. Для того чтобы иметь возможность осуществлять оптимальное автоматизированное проектирование систем теплоснабжения жилых зданий, необходимо иметь формальную модель, с помощью которой можно было бы решать задачу. Какие соображения должны быть положены в основу подобной модели? В настоящее время известны различные математические модели, используемые при проектировании систем теплоснабжения зданий и основанные на законах теплопередачи, например дифференциальные уравнения, линейные уравнения стационарного режима. Однако для большинства реальных задач использование классического подхода встречает серьезные препятствия, связанные со следующим. Во-первых, в рассмотрение при оптимизации должны быть включены показатели затрат, выраженные в виде эмпирических формул для расчета, например, стоимости жизненного цикла здания и других переменных, множество разнородных условий и требований, диктуемых действующими нормами и правилами. Во-вторых, при классическом подходе невозможно учесть требования, которые носят субъективный, присущий только данному проекту характер, и изменяются по мере продвижения процесса проектирования. В-третьих, упомянутый классический подход не охватывает метауровня, без которого современная автоматизация проектирования вообще неосуществима, а именно уровня планирования алгоритмов оптимального поиска в пространстве допустимых значений. Возможным путем частичного преодоления указанных препятствий является логический подход к решению задачи оптимального автоматизированного проектирования систем теплоснабжения зданий, в основе которого лежит комплексная онтология, которую для данного случая назовем онтологией теплоснабжения, включающая в себя весь багаж накопленных знаний. Пример компетентного прямого вопроса, на который может ответить онтология теплоснабжения: «Каковы будут эксплуатационные характеристики здания (например, комфортность и стоимость) при заданных значениях переменных здания и системы теплоснабжения (конструкции, применяемые материалы, цены)?» Пример компетентного обратного вопроса: «Каковы будут значения переменных конструкции, чтобы обеспечить требуемые эксплуатационные характеристики здания при заданных условиях (климатических, стоимостных т.п.)?» Можно выделить четыре группы аксиом онтологии теплоснабжения: а) аксиомы идентификации, получаемые по известным математическим уравнениям теплопередачи, формулам для расчета температуры, эмпирическим формулам для расчета стоимости жизненного цикла систем теплоснабжения, б) аксиомы вычислений, формулирующие правила вычисления значений искомых переменных, в) аксиомы корректности, задающие порядок и условия корректности вычислений, г) аксиомы оптимизации, позволяющие получать ответы на обратные вопросы и определяющие правила поиска оптимальных решений. Аксиомы идентификации. Полагаем, что здание в целом, включая систему теплоснабжения, имеет множество объектных переменных Введем множество отношений Введем переменную º экземпляр( Аксиомы вычислений. Следующий этап формирования онтологии – это формулировка аксиом вычислений, задающих правила вычисления отношений. Как уже отмечалось, каждое отношение параметр( Интервальная арифметика лежит в основе вычисления формул. Операции сложения, вычитания, умножения и деления над двумя интервалами [
[ [ [ [ 0Ï [
Рассмотрим пример аксиом вычислений для отношения сложения, связывающего три переменные множества а) вычисляющий по известным
(параметр( =[ (параметр( (параметр( =[
Аксиомы вычислений должны быть заданы для всех отношений. Аксиомы ограничений. Перед началом вычислений задается множество начальных значений входных переменных в виде множества предикатов параметр( Аксиомы оптимизации. Для того чтобы можно было получать ответы на обратные вопросы, необходимо иметь возможность нахождения оптимальных значений некоторых переменных, называемых критериями. Это означает, что в онтологии должна быть группа соответствующих аксиом оптимизации. Критериями, например, в нашем случае могут быть переменные комфортности и стоимость здания, причем для достижения энергетической эффективности стоимость должна учитывать все затраты жизненного цикла здания, т.е. расходы на эксплуатацию, энергию, ремонт. Это означает, что задача оптимизации является многокритериальной, а критерии - противоречивыми. В теории математического программирования такая задача ставится как векторная задача оптимизации с ограничениями. Среди объектных переменных, описывающих здание, выделим те, которые мы можем изменять в процессе поиска их оптимального сочетания. Они образуют вектор переменных Возможны три типа постановок задачи оптимального поиска: а) значения критериев комфортности задаются, а оптимизируется только стоимость, б) задается верхняя граница стоимости, которую нельзя превышать, а оптимизируются только критерии комфортности, в) совместно оптимизируются все критерии для поиска компромиссного решения. Первая задача является однокритериальной. Задачи “б” и “в” – многокритериальные, из которых наиболее общая – последняя. Рассмотрим подход к ее решению. Возможны методы решения многокритериальных задач, связанные с тем или иным учетом системы предпочтений человека и, на основе этого, с выбором какого-либо принципа оптимальности. Методы делятся на несколько групп: методы назначения весовых коэффициентов для каждого критерия, упорядочения критериев по важности, оптимизации наихудшего критерия, минимизации суммы отклонений критериев от идеальных значений и интерактивной оптимизации. Не во всех методах легко выразить предпочтения проектировщика и не все методы дают в конечном итоге оптимальное по Парето решение. Сущность методов оптимизации наихудшего критерия состоит в следующем. Решается задача оптимального поиска по каждому критерию Далее для каждого критерия определяется множество его относительных значений, вычисляемых по формуле! -! Частотное дискриминирование. В качестве второго примера рассмотрим задачу дискриминирования (сравнения) частот периодических последовательностей сигналов Математическая трактовка. Если частоты Выделим три класса частот
где 1) равные частоты –
2) кратные частоты –
где 3) минимально-некратные частоты –
где Соотношение (8.1) показывает, что аксиома вычисления результата сравнения
где
Приведенное значение
где
В этом случае
Математическая трактовка операции сравнения частот Алгоритм решения. Каким образом с помощью онтологий решить вторую часть задачи? Для этого определим вначале систему понятий алгоритма сравнения частот Определим обработку любых двух периодических последовательностей Рассмотрим вначале простейший случай, когда последовательность
|

 = =
= = 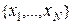 , включая все известные и неизвестные, исходные и промежуточные, оценочные и конструктивные. В реальном проектировании требуется находить и уточнять значения этих переменных, которые, как правило, должны попадать в определенный интервал. Интервалом в нашем случае назовем множество действительных чисел
, включая все известные и неизвестные, исходные и промежуточные, оценочные и конструктивные. В реальном проектировании требуется находить и уточнять значения этих переменных, которые, как правило, должны попадать в определенный интервал. Интервалом в нашем случае назовем множество действительных чисел  таких, что
таких, что  £
£  , где
, где 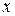 обозначим как [
обозначим как [  Í
Í  . Каждое отношение
. Каждое отношение  из
из  Í
Í  Í
Í  , значением которой является одно из конкретных отношений множества
, значением которой является одно из конкретных отношений множества 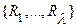 . Все появления одного и того же отношения перенумеруем и введем переменную
. Все появления одного и того же отношения перенумеруем и введем переменную  , значениями которой будут указанные номера. Введем также предикат экземпляр(
, значениями которой будут указанные номера. Введем также предикат экземпляр( ]) º
]) º ). Каждому такому разбиению сопоставим оператор
). Каждому такому разбиению сопоставим оператор  (
( ,
, 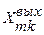 ),
),  =1, …,
=1, …,  Í
Í  [
[  ,
, 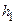 ])Ù …Ù параметр(
])Ù …Ù параметр( [
[  ,
, 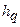 ])Ù Ù оператор(
])Ù Ù оператор( ,
,  ] имеют вид:
] имеют вид: отношением сложения
отношением сложения  . Для отношения сложения возможны только три оператора:
. Для отношения сложения возможны только три оператора: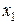 и
и  неизвестную
неизвестную  , б) вычисляющий по известным
, б) вычисляющий по известным  [
[  [
[  [
[  ,
,  ]))Ù ([
]))Ù ([  , [
, [  [
[  . Первый шаг вычисления – это нахождение тех предикатов типа экземпляр(
. Первый шаг вычисления – это нахождение тех предикатов типа экземпляр(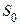 . После нахождения множества
. После нахождения множества 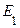 и все повторяется сначала, но вместо множества
и все повторяется сначала, но вместо множества  , … в принципе может продолжаться бесконечно. На практике останов происходит либо в результате появления на некотором этапе вычислений пустого множества, что соответствует отсутствию вычисляемых отношений, либо в результате предписанного заранее числа допустимых итераций, либо по достижении устраивающего пользователя результата, либо в результате каких-либо других критериев останова. Аксиомы, описывающие условия останова, называют аксиомами ограничений.
, … в принципе может продолжаться бесконечно. На практике останов происходит либо в результате появления на некотором этапе вычислений пустого множества, что соответствует отсутствию вычисляемых отношений, либо в результате предписанного заранее числа допустимых итераций, либо по достижении устраивающего пользователя результата, либо в результате каких-либо других критериев останова. Аксиомы, описывающие условия останова, называют аксиомами ограничений.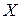 , конкретное значение которого!
, конкретное значение которого!  ,
,  с частотами следования соответственно
с частотами следования соответственно 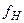 ,
,  . Данная задача распадается на две подзадачи: как математически сравнить частоты
. Данная задача распадается на две подзадачи: как математически сравнить частоты  /
/  =
=  /
/  , (8.1)
, (8.1) ,
,  =
=  -
-  , (8.5)
, (8.5) +
+  , (8.6)
, (8.6) . (8.7)
. (8.7) . (8.9)
. (8.9) Î
Î 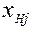 Î
Î  - номера элементов. Поскольку
- номера элементов. Поскольку  результат такого взаимодействия окажется также в виде последовательности
результат такого взаимодействия окажется также в виде последовательности  новых элементов, которые обозначим как
новых элементов, которые обозначим как  .
. Î
Î 


