Расчет балки на действие поперечных сил у опоры А
У опоры А при Asw = 2.28, 3 = 57 мм2 (2 Æ 6 А240), Максимально допустимый шаг поперечных стержней у опор в соответствии с п. 5.21 [3] при h 0 = 500 – 35 мм = 465 мм: s £ 0, 5 h 0 = = 0, 5 · 465 = 233 мм; s £ 300 мм. Кроме того, в соответствии с п. 3.35 [3]
Принимаем шаг поперечных стержней в каркасах s = 200 мм. Расчет прочности по полосе между наклонными сечениями. Расчет прочности по наклонной полосе между наклонными сечениями производим из условия 3.43 [2]. Q ≤ 0, 3 Rbbh 0, где Q принимается на расстоянии не менее h 0 от опоры 0, 3 Rbbh 0 = 0, 3· 7, 65·103 ·0, 25·0, 465 = 266, 8 кН > Q = = 83, 1 – 38, 37 · 0, 465 = 65, 26 кН, т. е. прочность наклонной полосы на сжатие обеспечена. Расчет прочности на действие поперечной силы по наклонному сечению.
(см. формулу (3.48) [3]). Так как qsw = 48, 45 кН/м > 0, 25 Rbtb = 0, 25·0, 675·1000·0, 25= 42, 19 кН/м, Mb = 1, 5 Rbtbh 02 =1, 5 · 0, 675 · 1000 · 0, 25 · 0, 4652 = = 54, 73 кН·м (см. п. 3.31 и формулу (3.46) [3]). Определяем длину проекции невыгоднейшего наклонного сечения c. При расчете элемента на действие равномерно распределенной нагрузки q значение c принимают равным
Так как
Принимаем длину проекции невыгоднейшего наклонного сечения c = 1, 19м. Длину проекции наклонной трещины c0 принимают равным c, но не более 2 h 0 = 0, 465 · 2= 0, 93м (см. п. 3.31 [3]). Принимаем длину проекции наклонной трещины c 0 = c = 0, 93м. Тогда
Поперечную силу, воспринимаемую бетоном, определяют по формуле
Qb , min = 0, 5 Rbbh 0 = 0, 5 · 0, 675 · 103 · 0, 25 · 0, 465 = 39, 23кН < < = 2, 5 · 0, 675 · 103 · 0, 25 · 0, 465 = 196, 2кН.
Принимаем Расчет изгибаемых элементов по наклонному сечению производят из условия
При Qsw + Qb = 33, 79 + 58, 85 = 92, 64 кН > Q = 54, 98 кН, т. е. прочность наклонных сечений у опоры А обеспечена (см. п. 3.31 [3]).
|

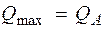 = 83, 1 кН.
= 83, 1 кН. =0, 44м.
=0, 44м.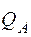 – qh 0 =
– qh 0 =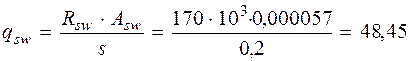 кН/м,
кН/м,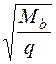 , а если при этом
, а если при этом 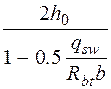 или
или 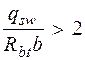 , следует принимать
, следует принимать (см. п. 3.32 [3]).
(см. п. 3.32 [3]).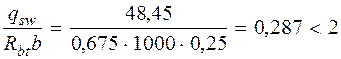 .
.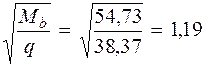 м >
м >  м,
м,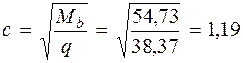 м, но не более 3 h 0 = 3 · 0, 465 = 1, 395 м (см. п. 3.32 [3]).
м, но не более 3 h 0 = 3 · 0, 465 = 1, 395 м (см. п. 3.32 [3]).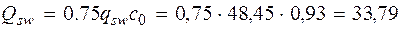 кН.
кН.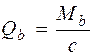 , но не более Qb , max = 2, 5 Rbtbh 0 и не менее Qb , min = 0, 5 Rbtbh 0 (см. п. 3.31 [3]).
, но не более Qb , max = 2, 5 Rbtbh 0 и не менее Qb , min = 0, 5 Rbtbh 0 (см. п. 3.31 [3]).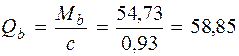 кН < Qb , max = 2, 5 Rbtbh 0 =
кН < Qb , max = 2, 5 Rbtbh 0 =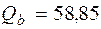 кН.
кН.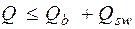 , где Q – поперечная сила в наклонном сечении с длиной проекции c; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем на расстоянии c от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной c.
, где Q – поперечная сила в наклонном сечении с длиной проекции c; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем на расстоянии c от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной c.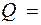
 = 83, 1 – 30, 24 · 0, 93 = 54, 98 кН.
= 83, 1 – 30, 24 · 0, 93 = 54, 98 кН.


