Расчет балки на действие поперечных сил у опор B и C
У опор В и С при Аsw = 28, 3 × 2 = 57 мм2 (2 Æ 6 А240). Максимально допустимый шаг поперечных стержней у опор в соответствии с п. 5.21 [3] при h 0 = 500 – 35 мм = 465 мм: s £ 0, 5 h 0 = = 0, 5 · 465 = 233 мм; s £ 300 мм. Кроме того, в соответствии с п. 3.35 [3]
Принимаем шаг поперечных стержней в каркасах s = 200 мм. Расчет прочности по полосе между наклонными сечениями. Расчет прочности по наклонной полосе между наклонными сечениями производим из условия 3.43 [2]. Q ≤ 0, 3 Rbbh 0, где Q принимается на расстоянии не менее h 0 от опоры 0, 3 Rbbh 0 = 0, 3· 7, 65 · 103 · 0, 25 · 0, 465 = 266, 8 кН > Q = У опоры В QB л = 124, 7 кН. При прочих равных параметрах (см. расчет по наклонному сечению у опоры А) проверим достаточность принятой поперечной арматуры по условию Q = При Qsw + Qb = 33, 79 + 58, 85 = 92, 64 кН < Q = 96, 88 кН, т. е. прочность наклонных сечений у опоры B недостаточна (см. п. 3.31 [3]). Увеличиваем диаметр поперечных стержней до 8 мм и оставляем шаг 200 мм. Тогда при Asw = 2 . 50, 3 = 101 мм2 (2 Æ 8 А240) снова проверяем прочность по наклонному сечению.
(см. формулу (3.48) [3]); Так как qsw = 85, 85 кН/м > 0, 25 Rbtb = 0, 25 · 0, 675 · 1000 · 0, 25= = 42, 19 кН/м, Mb = 1, 5 Rbtbh 02 = 1, 5 · 0, 675 · 1000 · 0, 25 · 0, 4652 = 54, 73 кН·м (см. п. 3.31 и формулу (3.46) [3]). Определяем длину проекции невыгоднейшего наклонного сечения c. При расчете элемента на действие равномерно распределенной нагрузки q значение c принимают равным
Так как
Принимаем длину проекции невыгоднейшего наклонного сечения c = 0, 73м. Длину проекции наклонной трещины c0 принимают равным c, но не более 2 h 0 = 0, 465 · 2= 0, 93 м (см. п. 3.31 [3]). Принимаем длину проекции наклонной трещины c 0 = c = 0, 73м. Тогда
Поперечную силу, воспринимаемую бетоном, определяют по формуле
Qb, min = 0, 5 Rbtbh 0 = 0, 5 · 0, 675 · 103 · 0, 25 · 0, 465 = 39, 23 кН < < = 2, 5 · 0, 675 · 103 · 0, 25 · 0, 465 = 196, 2 кН.
Принимаем Расчет изгибаемых элементов по наклонному сечению производят из условия
При Qsw + Qb = 47 + 74, 97 = 121, 97 кН > Q = 102, 62 кН, т. е. прочность наклонных сечений у опоры В обеспечена (см. п. 3.31 [3]). Согласно п.5.21 [3] шаг хомутов Sw у опоры должен быть не более h 0 / 2 = 465 / 2 = 232, 5 и 300 мм, а в пролете не более 0, 75 h 0 =348, 75 мм и 500 мм. Таким образом, окончательно устанавливаем во всех пролетах на приопорных участках длиной l/4 поперечную арматуру диаметром 8 мм с шагом 200 мм, а на средних участках с шагом 300 мм. У опоры В справа и у опоры С слева и справа при QBп = = – QС л < QB л и одинаковой поперечной арматуре прочность наклонных сечений также обеспечена.
Проверка прочности наклонного сечения у опоры А на действие момента. Поскольку продольная растянутая арматура при опирании на стену не имеет анкеров, расчет наклонных сечений на действие момента необходим. Принимаем начало наклонного сечения у грани опоры. Отсюда ls = l sup – 10 = 250 – 10 = 240 мм. Опорная реакция балки равна F sup = 83, 1 кН, а площадь опирания балки A sup = bl sup = 250 . 250 = 62500 мм2, откуда
σ b=
следовательно, α = 1. Из табл. 3.3 [3] при классе бетона В15, классе арматуры А400 и α = 1 находим λ an= 47. Тогда, длина анкеровки при ds= 22 ммравна lan = λ ands = 47 . 22 = 1034 мм.
Поскольку к растянутым стержням в пределах длины ls приварены 4 вертикальных и 1 горизонтальный поперечных стержня, увеличим усилие Ns на величину Nw. Принимая dw = 8 мм, nw = 5, φ w = 150 (см. табл. 3.4[3]), получаем
Отсюда Ns = 62623 + 22680 = 85303 Н. Определяем максимально допустимое значение Ns. Из табл. 3.3 [3] при α = 0, 7 находим λ an= 33; тогда
т. е. оставляем Ns = 85303 Н. Определим плечо внутренней пары сил
= 465 – 30 = = 435 мм.
Тогда момент, воспринимаемый продольной арматурой, равен
По формуле 3.48 [2] вычислим величину qsw
Определим длину проекции невыгоднейшего наклонного сечения по формуле 3.76 [3], принимая значение Q max равным опорной реакции балки
Тогда момент, воспринимаемый поперечной арматурой, равен
Момент в наклонном сечении определяем как момент в нормальном сечении, расположенном в конце наклонного сечения, т е. на расстоянии от точки приложения опорной реакции, равной x = l sup/3 + + c = 250/3 + 667, 2 = 750, 5мм
Проверяем условие 3.69 [2]
т. е. прочность наклонных сечений по изгибающему моменту обеспечена.
Расчет ширины раскрытия наклонных трещин. В учебном пособии этот расчет для второстепенной балки не производится. Аналогичный расчет выполнен для продольного ребра сборной ребристой панели. Определение ширины раскрытия нормальных трещин. Расчет производится в соответствии с п. 7.2.12 [2] на действие нормативных нагрузок. В учебном пособии этот расчет для второстепенной балки не производится. Аналогичный расчет выполнен для продольного ребра сборной ребристой панели.
|

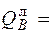 124, 7 кН; QВп = QC л= 110, 27 кН.
124, 7 кН; QВп = QC л= 110, 27 кН. = 0, 292 м.
= 0, 292 м.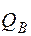 – – qh 0= 124, 7 – 38, 37 · 0, 465 = 106, 86 кН, т. е. прочность наклонной полосы на сжатие обеспечена.
– – qh 0= 124, 7 – 38, 37 · 0, 465 = 106, 86 кН, т. е. прочность наклонной полосы на сжатие обеспечена.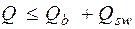 , где
, где кН/м
кН/м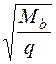 , а если при этом
, а если при этом 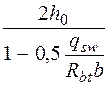 или
или 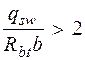 , следует принимать
, следует принимать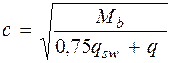 (см. п. 3.32 [3]).
(см. п. 3.32 [3]). .
.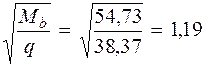 м <
м < 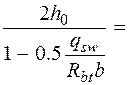
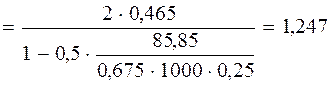 м,
м,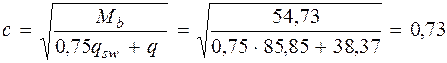 м, но не более 3 h 0 = = 3 · 0, 465 = 1, 395 м (см. п. 3.32 [3]).
м, но не более 3 h 0 = = 3 · 0, 465 = 1, 395 м (см. п. 3.32 [3]).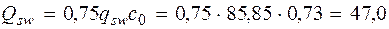 кН.
кН.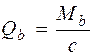 , но не более Qb, max = 2, 5 Rbtbh 0 и не менее Qb, min = 0, 5 Rbtbh 0 (см. п. 3.31 [3]).
, но не более Qb, max = 2, 5 Rbtbh 0 и не менее Qb, min = 0, 5 Rbtbh 0 (см. п. 3.31 [3]).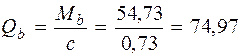 кН < Qb, max = 2, 5 Rbtbh 0 =
кН < Qb, max = 2, 5 Rbtbh 0 =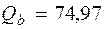 кН.
кН.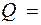
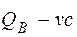 =124, 7 – 30, 24 · 0, 73= 102, 62 кН.
=124, 7 – 30, 24 · 0, 73= 102, 62 кН.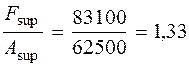 МПа,
МПа,  < 0, 25,
< 0, 25,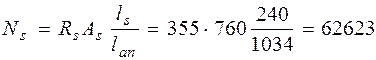 Н.
Н.
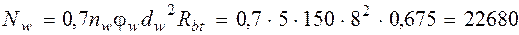 Н.
Н.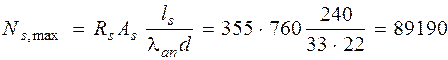 Н > 85303 Н,
Н > 85303 Н,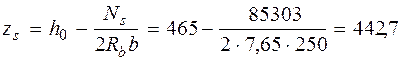 мм >
мм > 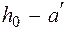 =
= Нмм.
Нмм.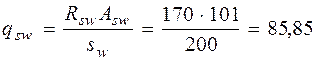 Н/мм.
Н/мм.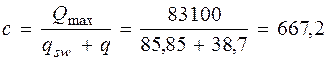 мм < 2 h 0 = 930 мм.
мм < 2 h 0 = 930 мм.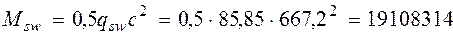 Нмм.
Нмм.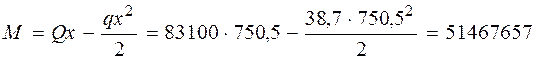 Нмм.
Нмм. Нмм > М =51467657 Нмм,
Нмм > М =51467657 Нмм,


