Определение преодолеваемого автомобилем сопротивления
Эта задача обратная предыдущей. Так, задав скорость движения, восстанавливаем ординату до пересечения с кривой D и проектируем точку на ось ординат. Например, скорости Va соответствует динамический фактор Dα (рис.16). Согласно формуле (65) для одиночной машины (Pкр = 0) при равномерном движении D = ψ.
С другой стороны нам известно, что по формуле (70) можно определить сопротивление движению
Ψ = fcosα + sinα;. (76)
Таким образом, задача может сводиться либо к определению коэффициента сопротивления качению (f) при заданном угле подъёма (α), то есть
либо к определению преодолеваемого угла подъёма при заданном сопротивлении. Используя уравнение (76) и (77), получим
Учитывая, что f 2 значительно меньше 1, формулу (78) можно упростить. Получим
Так, например, если автомобиль движется по мокрому суглинку (f= 0, 1 - 0, 2), то, как следует из рис.16, движение возможно на второй передаче со скоростями движения 8-20 км/ч, а также, если f ≤ 0, 1 и на третьей передаче со скоростями 20-25 км/ч. 6.Определение предельного угла преодолеваемого подъема
Пусть автомобиль движется по мокрому суглинку, как и в предыдущем случае, для которого принимаем коэффициент сопротивления качению f = 0, 125. При этом водитель включил в коробке передач первую передачу, а в раздаточной коробке низшую передачу (Dmax = 0, 6).
По формуле (79) получим
Таким образом, α тах = 30° . Для решения аналогичной задачи для поезда следует пользоваться динамической характеристикой поезда D∑ = f (V). При этом в формуле (79) вместо коэффициента сопротивления качению автомобиля необходимо подставить коэффициент сопротивления качению автопоезда.
|

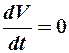 получим
получим (77)
(77)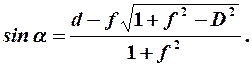 (78)
(78) (79)
(79)



