Определение ускорения автомобиля. Для определения ускорения одиночной машины при заданной скорости движения и заданном сопротивлении пользуемся выражением (75)
Для определения ускорения одиночной машины при заданной скорости движения и заданном сопротивлении пользуемся выражением (75)
Как видно из этой формулы, условием ускоренного движения является превышение динамического фактора над коэффициентом сопротивления движению (наличие запаса D ). При Следовательно, уравнение (75) дает текущее значение ускорения. В зависимости от того, возрастает или убывает динамический фактор, соответственно меняется и ускорение. Если ускорение убывает, то возможны два случая: либо ускорение станет равным нулю при Vн < Vk, тогда VH и будет возможной скоростью равномерного движения для данных условий; либо Исходя из этих соображений, решим конкретную задачу: определим величину максимального ускорения разгона на различных передачах с учётом того, что коэффициент сопротивления движению ψ = 0, 02. Для решения этой задачи пользуемся формулами (71) и (75). Для расчётов примем коэффициент учёта вращающихся масс колес В = 0, 04, а коэффициент учёта вращающихся масс двигателя А = 0, 0015. Результаты расчёта коэффициента вращающихся масс δ i на передачах сводим в табл.10.
Таблица 10 - Значения коэффициента вращающихся масс на передачах
Результаты расчёта максимальных значений ускорений на передачах сводим в табл.11.
Таблица 11 - Значения ускорений на передачах
Вывод: расчёты показывают, что разгон автомобиля при сопротивлении ψ = 0, 02 возможен. 8. Определение силы тяги на крюке
Возможная сила тяги на крюке определяется при равномерном движении ( Ркр =(D – ψ)G. (81)
Возможную тягу на крюке обычно определяют для расчётной точки, то есть в формуле (81) необходимо принимать D = Dp. В качестве примера определим силу тяги на крюке при скорости движения автомобиля Урал-4320 15 км/ч. При движении автомобиля на этой скорости, как видно из рис.16, в коробке передач должна быть включена вторая передача, а в раздаточной коробке - первая. По динамической характеристике получим, что D = Dp = 0, 18. Задаёмся другим условием: автомобиль движется по укатанной сухой грунтовой дороге, для которой ψ = 0, 020 + 0, 025. Принимаем ψ = 0, 02 В таком случае по формуле (81) получим
Ркр = (0, 18 - 0, 020) 13425 = 2150 кг.
|

 (80)
(80)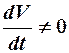 скорость машины изменяется, а поэтому динамический фактор и зависящее от него ускорение также будут переменными.
скорость машины изменяется, а поэтому динамический фактор и зависящее от него ускорение также будут переменными.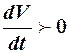 также и при скорости Vk, но при этом дальнейшее увеличение скорости всё равно невозможно, поскольку Vk соответствует предельной частоте вращения коленчатого вала двигателя. В этом случае VH =VK и равномерное движение будет происходить при неполном использовании мощности двигателя.
также и при скорости Vk, но при этом дальнейшее увеличение скорости всё равно невозможно, поскольку Vk соответствует предельной частоте вращения коленчатого вала двигателя. В этом случае VH =VK и равномерное движение будет происходить при неполном использовании мощности двигателя.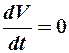 ) с заданными скоростью равномерного движения и заданным сопротивлением дороги. Решая уравнение (65) относительно искомой величины Ркр, получим
) с заданными скоростью равномерного движения и заданным сопротивлением дороги. Решая уравнение (65) относительно искомой величины Ркр, получим


