Точка и линия в плоскости

 

К числу основных задач, решаемых на плоскости, относят:

- проведение любой прямой в плоскости;

- построение в плоскости некоторой точки;

- построение недостающей проекции точки;

- проверка принадлежности точки и плоскости.

Решение этих задач основывается на известных положениях геометрии:

- прямая принадлежит плоскости, если она проходит через две точки, принадлежащих плоскости, или через точку в плоскости параллельно прямой, лежащей в этой плоскости;

- точка принадлежит плоскости, если через нее можно провести прямую, принадлежащую плоскости.

Рассмотрим примеры:

а) Проведение любой прямой в плоскости

 

Рисунок 18 – Произвольная прямая в плоскости

 

В плоскости АВС (рисунок 18) произвольно провести прямую через точку А. Она будет пересекать сторону ВС в точке 1. А111 – горизонтальная проекция прямой, фронтальную проекцию А212 достроить на основании принадлежности прямой и точки.

В плоскости АВС (рисунок 19) через точку В провести прямую параллельную стороне АС. Проекции прямой В212 и В111 параллельны стороне А2С2, А1С1.

 

Рисунок 19 – Параллельная прямая в плоскости

 

б) построение в плоскости некоторой точки

 

Рисунок 20 – Точка в плоскости

 

Построение точки в заданной плоскости сводится к двум операциям:

- построению в плоскости вспомогательной прямой;

- построению точки на этой прямой.

В плоскости, заданной прямой ВС (В₁С₁; В₂С₂) и точкой А (А₁; А₂) (рисунок 20), проводим вспомогательную прямую АD (A₁D₁; A₂D₂) пересекающую прямую ВС (В₁С₁; В₂С₂)вточке 1 (1₁; 1₂). Полученные точки 1 и D принадлежат плоскости.

в) построение недостающей проекции точки

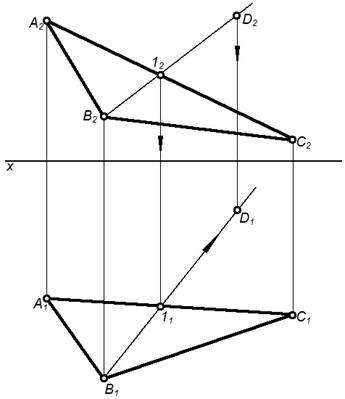
Рисунок 21 – Построение недостающей проекции точки

 

Плоскость задана проекциями треугольника АВС (А₁В₁С₁, А₂В₂С₂) (рисунок 21). Принадлежащая этой плоскости точка D задана проекцией D2. Следует достроить горизонтальную проекцию точки D (D₁), для этого проводят вспомогательную прямую В₂D_2, проходящую через точку 1₂ принадлежащую А₂В₂С₂. Затем на плоскости П₁ достраивают её горизонтальную проекцию 1₁ и соединяют ее с точкой В₁. На прямой В111 отмечают D₁.

г) проверка принадлежности точки плоскости.

Для проверки в плоскости используют вспомогательную прямую, принадлежащую плоскости.

На рисунке 22 плоскость задана параллельными прямыми АВ (А1В1; А2В2) и СD (С1D1; С2D2), и задана точка Е (Е2, Е1). Проводим через Е2 прямую 1222. Убеждаемся, что горизонтальная проекция Е(Е1) не принадлежит 1121. Следовательно, точка Е не принадлежит плоскости.

Рисунок 22 – Принадлежность точки плоскости