Метод проекций. Виды проецирования
Для построения изображения геометрических образов на плоскости пользуются методом проецирования. Проекция – это отображение геометрического образа на плоскость проекций, полученное при помощи аппарата центрального или параллельного проецирования. Пример центрального проецирования (рисунок 1): 1) точка S – центр проецирования; 2) плоскость П1 – плоскость проекции, не проходящая через S. 3) точка А - геометрический образ. Проводим через S и A прямую, которая называется проецирующей, до пересечения с плоскостью П1, найдем точку А1, которая является проекцией точки А на плоскости П1.
Рисунок 1 - Центральное проецирование
Пример параллельного проецирования: 1) S - направление проецирования (S – удалена в бесконечность); 2) П1 - плоскость проекции; 3) А и В – геометрические образы. При параллельном проецировании проецирующие линии (лучи) составляют с плоскостью проекций один и тот же угол. Если направление S и, следовательно, проецирующие линии перпендикулярны плоскости проекции, то способ проецирования называется прямоугольным, а полученные проекции прямоугольными или ортогональными.
Рисунок 2 - Параллельное проецирование
Одна проекция объекта проецирования (точки, прямой, плоскости или поверхности) не определяет его положения в пространстве, для определения положения объекта необходимо иметь не менее двух его проекций. С этой целью строят прямоугольные проекции геометрических образов на две или три взаимно перпендикулярные плоскости проекций. Прямоугольный метод проецирования на две или три взаимно перпендикулярные плоскости является основным методом начертательной геометрии. По этому методу изготовляются все технические чертежи. 2 Инвариантные свойства ортогонального (прямоугольного) проецирования
При параллельном ортогональном проецировании, в общем случае, нарушается метрическое равенство между оригиналом и его проекцией, хотя проекция сохраняет некоторые свойства оригинала, которые называются инвариантными (неизменяемыми): 1. Проекция точки есть точка: А®Ап 2. Проекция прямой на плоскость есть прямая: L(AB)®Lп(AпBп) 3. Если точка принадлежит линии, то проекция этой точки принадлежит проекции линии: АÎ LÞ AпÎ Lп 4. Проекции взаимно ç ç прямых также взаимно ç ç, а отношение отрезков таких прямых равно отношению их ç ç проекций.
5. Точка пересечения, проекций пересекающихся прямых является проекцией точки пересечения этих прямых: аÇ b=MÞ aпÇ bп=Мп 6. Плоская фигура, параллельная плоскости проекции проецируется на эту плоскость без искажений. 7. Плоский прямоугольник в общем случае проецируется в многоугольник с тем же числом вершин. Если плоскость многоугольника параллельна направлению проецирования, то она проецируется в прямую линию. 8. Параллельный перенос оригинала или плоскости проекций не изменяет вида и размеров проекций оригинала. 9. Если хотя бы одна из сторон прямого угла параллельна какой-либо плоскости проекций, то на эту плоскость прямой угол проецируется без искажений. Точка Прямоугольной проекцией точки на плоскость называется основание перпендикуляра, опущенного из точки на плоскость проекции. В качестве плоскостей проекций возьмем три взаимно перпендикулярные плоскости П1, П2, П3 (Рисунок 3). Плоскость П1, называется горизонтальной плоскостью проекций; плоскость П2 – фронтальной плоскостью проекций; плоскость П3 – профильной плоскостью проекций. X, Y, Z – оси проекций; О – начало координат. Проецирующие линии: АА1 ^ П1, АА2 ^ П2, АА3 ^ П3.
Рисунок 3 – Проецирование точки А на 3 плоскости проекций
Остальные линии чертежа называются линиями связей проекций. Название проекций точки А: А1 – горизонтальная проекция; А2 – фронтальная проекция; А3 – профильная проекция. Для получения комплексного чертежа следует совместить плоскости П1 и П3 с плоскостью П2, вращая их вокруг соответствующих осей. При этом следует убрать из пространственной модели точку А и проецирующие лучи, а оставить только линии связи.
Рисунок 4 - Комплексный чертеж точки
Комплексным чертежом (рисунок 4) называется чертеж, составленный из комплекса проекций точки, связанных между собой. Для удобства решения задач в дальнейшем поля проекций П1, П2, П3 ограничиваться не будут. Ось X на комплексном чертеже обозначается X12, так как она принадлежит одновременно двум плоскостям проекции: П1 и П2. Ось Z обозначается Z23, т.к. она принадлежит П2 и П3. Ось Y на П1 обозначается Y1, на П3 – Y3. Центр координат на комплексном чертеже обозначается О123. Фронтальная и горизонтальная проекции точки располагаются на одной вертикальной линии связи – А1А2 ^ X12. Фронтальная и профильная проекция точки расположены на одной линии связи – А2А3 ^ Z23. При наличии двух проекций точки, третью проекцию можно найти с помощью прямой - Ко, которая называется постоянной прямой комплексного чертежа. При безосном способе изображения положение осей проекций становится неопределенным и они на комплексном чертеже не наносятся. Комплексный чертеж точки приобретает вид, показанный на рисунке 5. Условие связи между проекцией те же, что и при осном способе изображения.
Рисунок 5 – Безосный чертеж точки
Определение пространственного положения точки можно осуществить при помощи ее прямоугольных координат. Координатами точки являются числа, выражающие расстояние от точки до трех взаимно перпендикулярных плоскостей проекций. Широта точки – расстояние от точки А до плоскости П3; обозначается Xа. Широта точки читается на П1 и П2. Глубина точки – расстояние от точки А до плоскости П2; обозначается Yа. Глубина точки читается на П1 и П3. Высота точки – расстояние от точки А до плоскости П1; обозначается Zа. Высота точки читается на П2 и П3. При прямоугольном проецировании возможны случаи, когда две точки имеют одинаковую координату. В этом случае на двух плоскостях проекций они лежат на одной линии связи, а на третьей плоскости проекций – проекции этих точек совпадают (одна из них закрывается другой). Такие точки называются конкурирующими точками.Конкурирующие точки могут быть на П1, П2 и П3. В каждом из этих случаев важно знать условия видимости конкурирующих точек: 1. Из двух горизонтально конкурирующих точек на П1 видна та, которая выше (у которой больше высота). 2. Из двух фронтально конкурирующих точек на П2 видна та, которая ближе (у которой больше глубина). 3. Из двух профильно конкурирующих точек на П3 видна та, у которой больше широта. Выводы: 1. Совокупность двух и более взаимосвязанных, ортогональных проекций геометрической фигуры, расположенных на одной плоскости чертежа, называется комплексным чертежом. 2. Обратимый комплексный чертеж должен содержать не менее двух проекций геометрической фигуры.
Прямая Прямая линия может быть задана в пространстве любыми двумя точками (например А и В рисунок 6). Построение проекций прямой на плоскость сводится к построению проекций её концевых точек, соединенными между собой прямыми линиями А1В1 и А2В2. Прямая общего положения – это прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций. На комплексном чертеже (рисунок 6) все её проекции расположены под углом к линиям связи, причем этот угол не равен 900.
Рисунок 6 – Комплексный чертеж прямой общего положения
На чертежах, применяемых в технике, нет надобности устанавливать расстояние точек изображаемого объекта до плоскостей проекций. Важно показать их взаимное расположение, поэтому необходимость задания осей проекций на комплексном чертеже во многих случаях отпадает. Рисунок 7 – безосный комплексный чертеж прямой, на котором отсутствуют оси координат (не зафиксированы плоскости проекций), следовательно, нет координат точек, но есть разности координат.
Рисунок 7 – Положение точек относительно друг друга
Прямые параллельные или перпендикулярные к какой-либо плоскости проекций называются прямыми частного положения. Линии уровня Прямая параллельная какой-либо плоскости проекций называется линией уровня (рисунок 8): а) прямая АВ параллельна П1 ее называют горизонталью. Проекция на П2 - А2В2 параллельна оси X, перпендикулярна вертикальным линиям связи; проекция на П1 - А1В1 натуральная величина самого отрезка, β – угол наклона АВ к П2; б) прямая СD параллельна П2 ее называют фронталью. Проекция на П1 - С1D1 параллельна оси X, перпендикулярна вертикальным линиям связи; проекция на П2 - С2 D2 натуральная величина самого отрезка, α – угол наклона СD к П1; в) прямая EF параллельна П3 ее называют профильной прямой. Проекция на П2 - E2F2 параллельна Z, на П1 - E1 F1 параллельна Y, совпадает с вертикальной линией связи, проекция на П3 - E3F3 натуральная величина самого отрезка, α и β углы наклона к П1 и П2. Проецирующие прямые Прямая перпендикулярная к какой-либо плоскости проекций, называется проецирующей прямой (рисунок 8): г) прямая АВ перпендикулярна к П1 ее называют горизонтально-проецирующей прямой. Проекция на П1 точка А1=В1 , обладает собирательным свойством, на П2 и П3 проецируется в натуральную величину; д) прямая ЕF перпендикулярна к П2 ее называют фронтально-проецирующей прямой. Проекция на П2 точка Е2=F2, обладает собирательным свойством, на П1 и П3 проецируется в натуральную величину; е) прямая ЕD перпендикулярна к П3 ее называют профильно-проецирующей прямой. Проекция на П3 точка Е3=D3, обладает собирательным свойством, на П1 и П2 проецируется в натуральную величину.
а) г)
б) д)
в) е)
Рисунок 8 – Прямые частного положения
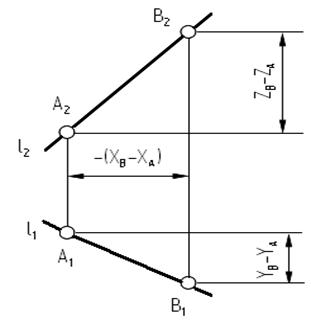
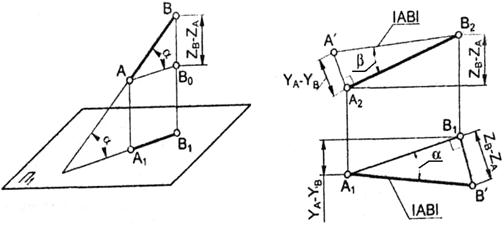
Таким образом, можно видеть, что прямые уровня и проецирующие прямые на комплексном чертеже всегда имеют одну из проекций, которая равна натуральной величине отрезка. Несложно так же определить и углы наклона таких прямых к плоскостям проекций. Для определения натуральной величины прямой общего положения и угла ее наклона к плоскости проекций пользуются способом прямоугольного треугольника (рисунок 9).
а) б)
Рисунок 9 – Способ прямоугольного треугольника
Построим ортогональную проекцию А1В1 отрезка АВ на плоскости P1. Проведем АВ0 параллельную А1В1. Треугольник АВВ0 - прямоугольный (рисунок 9а) длина одного его катета равна длине горизонтальной проекции отрезка АВ, а второго – разности высот точек АВ. Отрезок АВ является гипотенузой этого треугольника, а угол a - углом наклона АВ к P1. Треугольник конгруэнтный данному, можно построить на комплексном чертеже (рисунок 9б). Приняв А1В1 за один катет, строим прямоугольный треугольник, вторым катетом которого является отрезок В1В\ = ZВ – ZА – разность высот. Длина гипотенузы А1В\ равна натуральной величине АВ, а угол a = В1А1В\ – величине угла наклона его к P1. Длина отрезка может быть определена как длина гипотенузы прямоугольного треугольника, одним катетом которого является фронтальная проекция А2В2, а вторым – разность глубины А и В (это построение также показано на рисунке 9б). Гипотенуза А\В2 – натуральная величина АВ, а угол b - А\В2А2 – величина угла наклона отрезка АВ к P2.
|