Прискорення
Рух з незмінною швидкістю відбувається досить рідко. В більшості випадків швидкість руху міняється як за величиною, так і по напряму. Зміна швидкості характеризується прискоренням. При русі тіла по криволінійній траєкторії його швидкість Вектор зміни швидкості
Рисунок 1.4. Миттєвим прискоренням (чи просто прискоренням)
Таким чином, прискорення являється векторною величиною, і дорівнює першій похідній швидкості за часом. За одиницю прискорення приймають 1м/с2. Напрям вектора прискорення
Рисунок 1.5. Дотичне (тангенціальне) прискорення вказує, як швидко змінюється швидкість тіла по модулю:
Вектор Нормальне прискорення вказує, як швидко швидкість тіла змінюється по напряму. Вектор нормального прискорення Криволінійний рух можна представити як рух по дугах кіл (рис. 1.6). Вектор нормального прискорення спрямований по радіусу до центру кола. Його називають ще доцентровим прискоренням. Модуль доцентрового прискорення пов'язаний з лінійною швидкістю співвідношенням:
Рисунок 1. 6. Таким чином, при русі матеріальної точки по криволінійній траєкторії вектор прискорення геометрично складається з прискорення тангенціального, спрямованого по дотичній до траєкторії руху і прискорення нормального, спрямованого по головній нормалі до центру кола.
Модуль вектора прискорення визначається по теоремі Піфагора
Приклад розв’язку задачі. Точка рухається по осі Х згідно із законом х = 2 + 5t +2 t2, де t в секундах, а х - в метрах. Визначити координату, швидкість і прискорення цієї точки у момент часу t= 2с. 1. Для знаходження координати точки у момент часу 2 с потрібно в рівняння рух підставити цей момент часу. Х(2) = 2 + 5·2 +2 ·22=20 м. 2. Для знаходження швидкості точки у момент часу 2с необхідно отримати рівняння швидкості (залежність швидкості руху від часу) і підставити в це рівняння момент часи 2 с. Так, як рух відбувається уздовж осі Х V=VX V(t)=5+4·2=13 м/с. 3. Для знаходження прискорення точки у момент часу 2с необхідно отримати рівняння прискорення (залежність прискорення руху від часу) і підставити в це рівняння момент часи 2 с. Так, як рух прямолінійний повне прискорення дорівнює тангенціальному прискоренню
Рух тіл з прискоренням вільного падіння Вільним падінням тіл називають падіння тіл на Землю у відсутність опору повітря (у порожнечі). У кінці XVI століття знаменитий італійський вчений Галілео Галілей дослідним шляхом встановив, що у відсутність опору повітря усі тіла падають на Землю рівноприскорено, і що в даній точці Землі прискорення усіх тіл при падінні одне і те ж. До цього впродовж майже двох тисяч років, починаючи з Аристотеля, в науці було прийнято вважати, що важкі тіла падають на Землю швидше за легких. Прискорення, з яким падають на Землю тіла, називається прискоренням вільного падіння. Вектор прискорення вільного падіння позначається символом g. Він спрямований по вертикалі вниз. У різних точках земної кулі залежно від географічної широти і висоти над рівнем моря числове значення g виявляється неоднаковим, змінюючись приблизно від 9, 83 м/с2 на полюсах до 9, 78 м/с2 на екваторі. У наших широтах g = 9, 81523 м/с2. Зазвичай, якщо в розрахунках не потрібно високу точність, то приймають численне значення g у поверхні Землі рівним 9, 8 м/с2, або навіть 10 м/с2.
|

 змінюється за величиною і напрямом. Зміна вектора швидкості
змінюється за величиною і напрямом. Зміна вектора швидкості 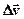 (рис.1.4).
(рис.1.4).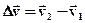 , можна розкласти на дві складові:
, можна розкласти на дві складові:  (дотичну або тангенціальну складова), спрямовану уздовж вектора
(дотичну або тангенціальну складова), спрямовану уздовж вектора 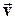 , і
, і 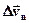 (нормальну складову), спрямовану перпендикулярно вектору
(нормальну складову), спрямовану перпендикулярно вектору 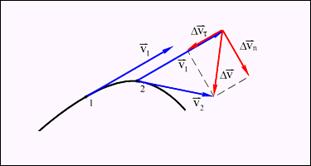
 тіла називають межу відношення малої зміни швидкості
тіла називають межу відношення малої зміни швидкості 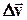 до малого проміжку часу Δ t, впродовж якого відбувалася зміна швидкості, або похідну від швидкості за часом:
до малого проміжку часу Δ t, впродовж якого відбувалася зміна швидкості, або похідну від швидкості за часом: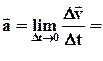
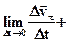

 . (1.4)
. (1.4)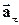 ) і прискорення по головній нормалі (нормальне прискорення
) і прискорення по головній нормалі (нормальне прискорення 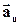 ) (рис.1. 5).
) (рис.1. 5).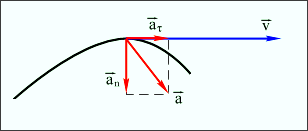
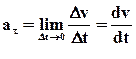 . (1.5)
. (1.5) . (1.6)
. (1.6)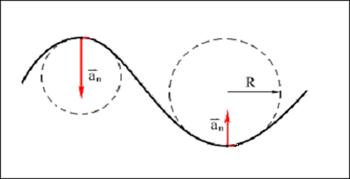
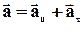 .
. . (1.7)
. (1.7)
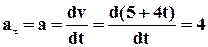 м/с2.
м/с2.


