Сигналы с импульсной модуляцией

 

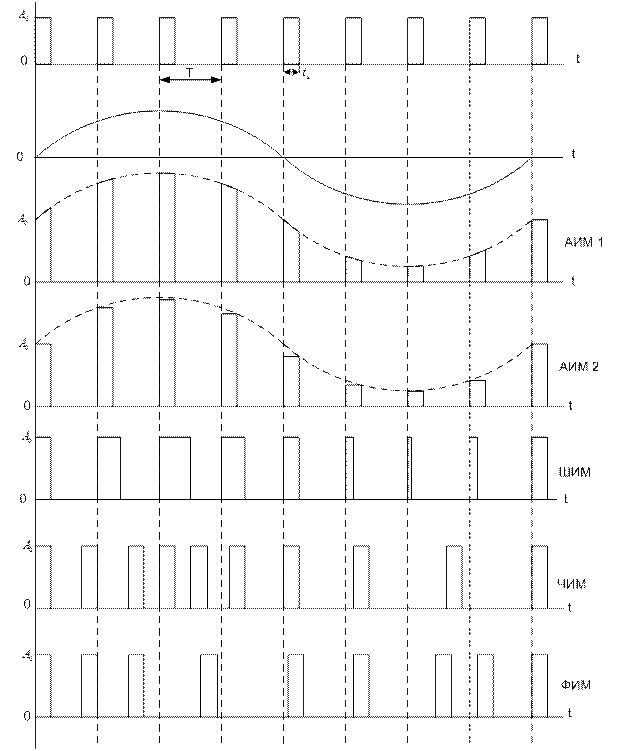
При импульсной модуляции в качестве несущего колебания используется последовательность импульсов.

 

 

АИМ: АИМ-1 и АИМ-2

При АИМ-1 мгновенное значение амплитуды импульса изменяется в соответствии с изменением входного сигнала. При АИМ-2 амплитуда импульсов определяется значением входного сигнала в тактовые моменты и остаётся постоянной во время передачи импульса.

При ШИМ модулируется положение одного из фронтов импульсов, при двусторонней ШИМ – относительно центра импульса симметрично смещаются оба фронта.

При ФИМ форма импульсов в процессе модуляции остаётся неизменной, а пропорционально мгновенному значению модулированного сигнала изменяется положение импульса в пределах тактового интервала.

ЧИМ характеризуется тем, что в зависимости от мгновенного значения входного сигнала изменяется частота следования импульсов.

Раздел 6. Основы теории случайных процессов

Случайные процессы. Основные понятия и определения

 

Теория случайных величин изучает вероятностные явления «в статике», рассматривая их как некоторые зафиксированные результаты экспериментов. Для описания сигналов, которые отображают развивающиеся, во времени случайные явления, методы классической теории вероятностей оказываются недостаточными. Подобные задачи изучает особая ветвь математики, получившая название теории случайных процессов.

По определению, случайный процесс x(t) – это особого вида функция, характеризующаяся тем, что в любой момент времени t принимаемые ею значения является случайными величинами.

Детерминированные сигналы мы отображаем их функциональными зависимостями или осциллограммами. Если же речь идёт о случайных процессах, то фиксируя на определённом промежутке времени мгновенные значения случайного сигнала, мы получаем лишь единственную реализацию случайного процесса. Случайный процесс представляет собой бесконечную совокупность таких реализаций, образующих статистический ансамбль. Например, ансамблем является набор сигналов , которые можно одновременно наблюдать на выходах совершенно одинаковых генераторов шумового напряжения или на выходах много канальной системы связи.

Совсем необязательно, чтобы реализации случайного процесса представлялись функциями со сложным, нерегулярным во времени поведением. Часто приходится рассматривать случайные процессы, образованные, например, всевозможными гармоническими сигналами , у которых один из трёх параметров 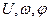- случайная величина, принимающая определённое значение в каждой реализации. Случайный характер такого сигнала заключен в невозможности заранее до опыта знать значение этого параметра.

Случайные процессы, образованные реализациями, зависящими от конечного числа параметров, принято называть квазидетерминированными случайными процессами.