Автокорреляционная функция сигналов
Задача корреляционного анализа возникла из радиолокации, когда нужно было сравнить одинаковые сигналы, смещённые во времени. Для количественного определения степени отличия сигнала U(t) и его смещённой во времени копии
Свойства АКФ 1) При
2) АКФ – функция чётна
3) Важное свойство автокорреляционной функции состоит в следующем: при любом значении временного сдвига
4) Обычно, АКФ представляется симметричной линей с центральным максимумом, который всегда положителен. При этом в зависимости от вида сигнала U(t) автокорреляционная функция может иметь как монотонно убывающей, так и колеблющийся характер. Например: АКФ прямоугольного видеоимпульса
АКФ пачки из трёх прямоугольных видеоимпульсов, сдвинутых друг относительно друга на время T.
АКФ бесконечной периодической последовательности видеоимпульсов:
Существует тесная связь между АКФ и энергетическим спектром сигнала. В соответствии с формулой (4.8) АКФ есть скалярное произведение Обратившись к теореме Планшереля – можно записать равенство:
Спектральная плотность смещённого во времени сигнала
Квадрат модуля спектральной плотности представляет собой энергетический спектр сигнала. Итак энергетический спектр и автокорреляционная функция связаны парой преобразований Фурье.
Ясно что имеется и обратное соотношение
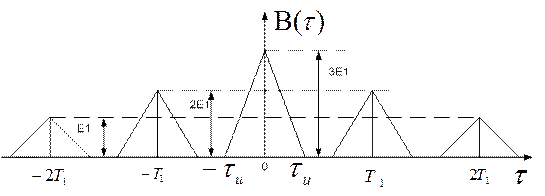
Эти результаты принципиально важны по двум причинам: во-первых оказывается возможным оценивать корреляционные свойства сигналов, исходя из распределения их энергии по спектру. Во-вторых, формулы (4.12), (4.13) указывают путь экспериментального определения энергетического спектра. Часто удобнее вначале получить АКФ, а затем, используя преобразование Фурье, найти энергетический спектр сигнала. Такой приём получил распространение при исследовании свойств сигналов с помощью быстродействующих ЭВМ в реальном масштабе времени. Часто вводят удодный числовой параметр – интервал корреляции Например:
В данном случае: Отсюда: Интервал корреляции тем меньше, чем выше верхняя граничная частота спектра сигнала. (Чем шире полоса частот сигнала тем уже основной лепесток АКФ.)
|

 принято вводить автокорреляционную функцию (АКФ) сигнала U(t), равную скалярному произведению сигнала и его сдвинутой копии.
принято вводить автокорреляционную функцию (АКФ) сигнала U(t), равную скалярному произведению сигнала и его сдвинутой копии. (4.8)
(4.8)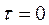 автокорреляционная функция становится равной энергии сигнала:
автокорреляционная функция становится равной энергии сигнала: (4.9)
(4.9) (4.10)
(4.10) модуль АКФ не превосходит энергии сигнала:
модуль АКФ не превосходит энергии сигнала:

 . Здесь символом
. Здесь символом  обозначена смещённая во времени копия сигнала
обозначена смещённая во времени копия сигнала  .
.
 , откуда
, откуда  . Таким образом приходим к результату
. Таким образом приходим к результату (4.12)
(4.12)
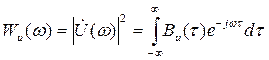 (4.13)
(4.13) , представляющий собой оценку ширины основного лепестка АКФ.
, представляющий собой оценку ширины основного лепестка АКФ.


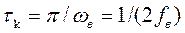 (4.14)
(4.14)


