Взаимная спектральная плотность сигналов. Энергетический спектр
Пусть имеется два вещественных сигнала U(t) и V(t). Назовём взаимным энергетическим спектром двух вещественных сигналов функцию такую что:
причём:
Взаимный энергетический спектр
где
Последняя формула даёт возможность проанализировать взаимосвязь сигналов. Более того формула (4.5) указывает путь, позволяющий уменьшить связи между двумя сигналами, добившись в пределе их ортогональности. Для этого один из сигналов нужно подвергнуть обработке частотным фильтром. К этому фильтру предъявляется требование не пропускать на выход спектральные составляющие, находящиеся в пределах частотного интервала, где вещественная часть взаимного энергетического спектра велика. Частотная зависимость к-та передачи такого сигнала ортогонализирующего фильтра будет обладать резко выраженным минимумом в пределах указанной области частот.
Если в формуле (4.1) сигналы U(t) и V(t) считать одинаковыми то эта формула приобретает вид:
Величина
Подход, основанный на спектральном представлении энергии сигнала, выгодно отличается относительной простотой. Энергии, отвечающие различным областям частотной оси, складываются так же, как вещественные числа. Однако, изучая сигнал с помощью его энергетического спектра, мы неизбежно теряем информацию, которая заключается в фазовом спектре сигнала, поскольку в соответствии с формулой (4.6) энергетический спектр есть квадрат модуля спектральной плотности и не зависит от её фазы. Однако понятие энергетического спектра широко применяется для инженерных оценок, устанавливающих ширину спектра сигнала и копи:
|

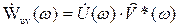 (4.1)
(4.1) (4.2)
(4.2) (4.3)
(4.3) - функция, принимающая в общем случае, комплексные значения:
- функция, принимающая в общем случае, комплексные значения: (4.4)
(4.4) - чётная, а
- чётная, а  нечётная функция частоты. Вклад в интеграл даёт только вещественная часть, поэтому:
нечётная функция частоты. Вклад в интеграл даёт только вещественная часть, поэтому: (4.5)
(4.5)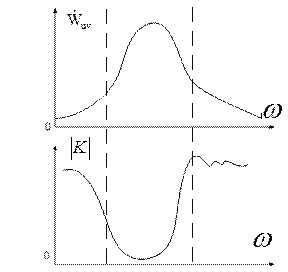
 (4.6)
(4.6) носит название спектральной плотности энергии сигнала U(t) или, короче, его энергетического спектра. Формула равенства Парсеваля при этом запишется так:
носит название спектральной плотности энергии сигнала U(t) или, короче, его энергетического спектра. Формула равенства Парсеваля при этом запишется так: (4.7)
(4.7)


