Аналитический сигнал и преобразования Гильберта
Анализируя формулу обратного преобразования Фурье, приходим к выводу, что произвольный сигнал S(t) с известной спектральной плотностью
Назовём функцию:
аналитическим сигналом, отвечающим колебанию S(t). Первый из интегралов в правой части формулы (3.26) путём замены переменной
(3.28) Поэтому формула (3.26) устанавливает связь между сигналами S(t) и или:
Называется сопряжённым сигналом по отношению к исходному колебанию S(t). Итак аналитический сигнал:
На комплексной плоскости этот сигнал отображается вектором, модуль и фазовый угол которого изменяются во времени. Проекция аналитического сигнала на вещественную ось в любой момент времени равна исходному сигналу S(t). Исследуем спектральную плотность аналитического сигнала. Пусть Если
Спектральная плотности исходного и сопряжённого сигналов связаны между собой следующим образом:
Чтобы на практике получить сопряжённый сигнал, необходимо исходное колебание S(t) подать на вход некоторой системы, которая осуществляет поворот фаз всех спектральных составляющих на угол - Для удобства вычислений представим эту функцию в виде предела:
Тогда:
Таким образом сопряжённый сигнал связан с исходным сигналом соотношением:
Можно поступить и по иному, выразив сигнал S(t) через
Поэтому соответствующая формула будет отличаться от (3.35) лишь знаком:
Формулы (3.35) и (3.36) называются прямым и обратным преобразованием Гильберта. Символическая запись его такова:
Функция Свойства преобразований Гильберта. 1) Простейшее свойство – линейность. 2) Сигнал, сопряжённый к константе, тождественно равен нулю: 3) Важное свойство преобразования Гильберта состоит в следующем: если при каком-либо t исходный сигнал S(t) достигнет экстремума(максимума или минимума), то в окрестности этой точки сопряжённый сигнал проходит через нуль. Если исходный сигнал изменяется во времени «подобно косинусу», то сопряжённый с ним сигнал изменяется «подобно синусу». 4) Преобразования Гильберта имеют нелокальный характер: в общем случае поведение сопряженного сигнала в окрестности какой-либо точки, зависит от свойств исходного сигнала на всей оси времени.
Некоторые применения преобразований Гильберта 1) Преобразования Гильберта для гармонических сигналов 2) Преобразования Гильберта для узкополосного сигнала. Пусть известна функция
Первое слагаемое в правой части соответствует области частот
Откуда видно, что спектральная плотность комплексной огибающей сопряжённого сигнала.
Сопряжённый сигнал в данном случае так же является узкополосным. Если комплексная огибающая исходного сигнала: Отсюда следует что узкополосному сигналу:
3) Преобразование Гильберта огибающей, полной фазы и мгновенной частоты. В рамках метода преобразования Гильберта огибающая
По определению полная фаза любого сигнала S(t) равна аргументу аналитического сигнала
Мгновенная частота
Зная аналитический сигнал можно определить огибающую и мгновенную частоту узкополосного сигнала, не применяя искусственное понятие опорной частоты. Кроме того, формулы (3.44, 3.45, 3.45) сохраняют смысл и применительно к сигналам произвольного вида. Согласно методу преобразований Гильберта, огибающая и мгновенная частота сигнала жёстко связаны друг с другом и их нельзя выбрать произвольно. Теория аналитического сигнала разработана выдающимся венгерским физиком Денешем Габором, лауреатом Нобелевской премии. Раздел 4. Основы корреляционного анализа сигналов
|

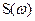 можно записать как сумму двух составляющих, каждая из которых содержит или только положительные, или только отрицательные частоты:
можно записать как сумму двух составляющих, каждая из которых содержит или только положительные, или только отрицательные частоты: (3.26)
(3.26) (3.27)
(3.27) преобразуется к виду:
преобразуется к виду:
 :
:  (3.29)
(3.29) - вещественная часть аналитического сигнала. Мнимая часть аналитического сигнала:
- вещественная часть аналитического сигнала. Мнимая часть аналитического сигнала: (3.30)
(3.30)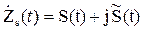 (3.31)
(3.31)

 - спектральная плотность сопряжённого сигнала, то в силу линейности преобразования Фурье:
- спектральная плотность сопряжённого сигнала, то в силу линейности преобразования Фурье: (3.32)
(3.32) (3.33)
(3.33) в области положительных частот и на угол
в области положительных частот и на угол  исходного сигнала и функции
исходного сигнала и функции  . В соответствии с обратной теоремой о свёртке сопряжённый сигнал представляет собой свёртку двух функций S(t) и f(t), которая является обратным преобразованием Фурье по отношении к функции
. В соответствии с обратной теоремой о свёртке сопряжённый сигнал представляет собой свёртку двух функций S(t) и f(t), которая является обратным преобразованием Фурье по отношении к функции 


 (3.34)
(3.34)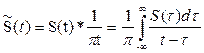 (3.35)
(3.35)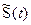 , который полагается известным. Для этого достаточно заметить, что из (3.33) вытекает следующая связь между спектральными плотностями.
, который полагается известным. Для этого достаточно заметить, что из (3.33) вытекает следующая связь между спектральными плотностями.
 (3.36)
(3.36)
 (3.37)
(3.37) называется ядром этих преобразований.
называется ядром этих преобразований. (3.38)
(3.38) (3.39)
(3.39)
 (3.40)
(3.40)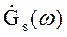 - спектральная плотность комплексной огибающей узкополосного сигнала S(t) с опорной частотой
- спектральная плотность комплексной огибающей узкополосного сигнала S(t) с опорной частотой  . Согласно формуле (3.25), спектр данного сигнала.
. Согласно формуле (3.25), спектр данного сигнала.
 , второе
, второе  . Тогда на основании формулы (3.33) спектр сопряжённого сигнала:
. Тогда на основании формулы (3.33) спектр сопряжённого сигнала: (3.41)
(3.41) (3.42)
(3.42) , то в соответствии с равенством (3.42) комплексная огибающая сопряжённого сигнала равна
, то в соответствии с равенством (3.42) комплексная огибающая сопряжённого сигнала равна  и отличается от комплексной огибающей исходного колебания лишь наличием постоянного фазового сдвига на
и отличается от комплексной огибающей исходного колебания лишь наличием постоянного фазового сдвига на  в сторону запаздывания.
в сторону запаздывания.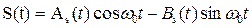 соответствует сопряжённый по Гильберту сигнал.
соответствует сопряжённый по Гильберту сигнал. (3.43)
(3.43) произвольного сигнала S(t) определяется как модуль соответствующего аналитического сигнала:
произвольного сигнала S(t) определяется как модуль соответствующего аналитического сигнала: (3.44)
(3.44) :
: (3.45)
(3.45) сигнала есть производная полной фазы по времени:
сигнала есть производная полной фазы по времени: (3.46)
(3.46)


