Взаимокорреляционная функция двух сигналов
Взаимокорреляционной функцией (ВКФ) двух вещественных сигналов U(t) и V(t) называется скалярное произведение вида:
ВКФ служит мерой «устойчивости» ортогонального состояния при сдвигах сигналов во времени. Действительно, если сигналы U(t) и V(t) ортогональны в исходном состоянии, то При прохождении этих сигналов через различные устройства возможно, что сигнал V(t) будет сдвинут относительно сигнала U(t) на некоторое время Свойства ВКФ. 1) В отличие от АКФ одиночного сигнала, ВКФ, описывающая свойства системы двух независимых сигналов, не является чётной функцией аргумента
2) Если рассматриваемые сигналы имеют конечные энергии, то их ВКФ ограничена. 3) При Пример ВКФ может служить взаимокорреляционная функция прямоугольного и треугольного видеоимпульсов.
Установим связь ВКФ со взаимной спектральной плотностью (взаимным энергетическим спектром) На основании теоремы Планшереля
и поскольку спектр смещённого во времени сигнала Поскольку
Таким образом, взаимокорреляционная функция и взаимный энергетический спектр связаны между собой парой преобразований Фурье. Если сигналы U(t) и V(t) – дискретные, то их можно задать как совокупность отсчётов, следующих во времени с одинаковыми интервалами T
Тогда по аналогии с АКФ одиночного сигнала ВКФ двух дискретных сигналов определится по формуле:
где n – целое число, положительное, отрицательное или нуль. Раздел 5. Модулированные сигналы
Чтобы осуществить эффективную передачу сигналов в какой-либо среде, необходимо перенести спектр этих сигналов из низкочастотной области в область достаточно высоких частот. Данная процедура получила в технике связи название модуляции. Прежде всего в передатчике формируется вспомогательный высокочастотный сигнал, называемый несущим колебанием. Его математическая модель Физический процесс управления параметрами несущего колебания и является модуляцией. Широкое распространение получили системы модуляции, использующие в качестве несущего простое гармоническое колебание.
имеющее три свободных параметра U,
|

 (4.18)
(4.18)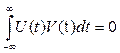
 .
. (4.19)
(4.19) значения ВКФ вовсе не обязаны достигать максимума.
значения ВКФ вовсе не обязаны достигать максимума.

 , то
, то  и
и 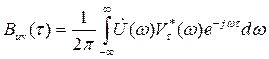 (4.20)
(4.20)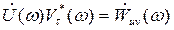 взаимный энергетический спектр то будет справедливо равенство:
взаимный энергетический спектр то будет справедливо равенство: (4.21)
(4.21)
 (4.22)
(4.22) , такова что имеется некоторая совокупность параметров
, такова что имеется некоторая совокупность параметров  ,
,  , …,
, …,  , определяющих форму этого колебания. Пусть S(t) – низкочастотное сообщение, подлежащее передаче по каналу связи на расстояние. Если по крайней мере, один из указанных параметров изменяется во времени пропорционально передаваемому сообщению, то несущее колебание приобретает новое свойство – оно несёт в себе информацию которая первоначально была заключена в сообщении S(t).
, определяющих форму этого колебания. Пусть S(t) – низкочастотное сообщение, подлежащее передаче по каналу связи на расстояние. Если по крайней мере, один из указанных параметров изменяется во времени пропорционально передаваемому сообщению, то несущее колебание приобретает новое свойство – оно несёт в себе информацию которая первоначально была заключена в сообщении S(t). , (5.1)
, (5.1)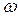 и
и 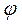 . Изменяя во времени тот или иной параметр, можно получать различные виды модуляции.
. Изменяя во времени тот или иной параметр, можно получать различные виды модуляции.


