Сигналы с угловой модуляцией
Будем изучать модулированные радиосигналы, которые получаются за счёт того, что в несущем гармоническом колебании Виды угловой модуляции. Предположим, что полная фаза
Где
Если сигнал S(t)=0, то ФМ – колебание является простым гармоническим колебанием. С увеличением значения сигнала S(t) полная фаза В моменты времени, когда сигнал S (t)достигает экстремальных значений, абсолютный фазовый сдвиг между ФМ-сигналом и немодулированным гармоническим колебанием оказывается наибольшим. Предельное значение этого фазового сдвига называется девиацией фазы
При частотной модуляции сигнала (414) между величинами S(t) и
Поэтому:
Естественными параметрами ЧМ-сигнала общего вида в соответствии с формулой (5.23) являются девиация частоты вверх Однотональные сигналы с угловой модуляцией. Анализ ФМ- и ЧМ-сигналов с математической точки зрения гораздо сложнее, чем исследование АМ-колебаний. Поэтому мы будем рассматривать простейшие однотональные сигналы. В случае однотонального ЧМ-сигнала мгновенная частота:
где На основании формулы (5.22) полная фаза такого сигнала
где Величина
называется индексом однотональной угловой модуляции. Для краткости положим, что неизменные во времени фазовые углы
Аналитическая форма записи однотонального ФМ-сигнала будет аналогичной. Однако нужно иметь в виду следующее: ЧМ- и ФМ-сигналы ведут себя по-разному при изменении частоты модуляции и амплитуды модулирующего сигнала, кроме того при ФМ
Спектральное разложение ЧМ- и ФМ-сигналов при малых индексах модуляции.
Задачу о представлении сигналов с угловой модуляцией посредством суммы гармонических колебаний несложно решить в случае, когда
Поскольку индекс угловой модуляции мал, воспользуемся приближёнными равенствами:
На основании этого из равенства (5.27) получаем:
Таким образом, показано, что при
Спектральная диаграмма сигнала с угловой модуляцией при
Для спектральной диаграммы, построенной по формуле (5.28) характерно то, что нижнее боковое колебание имеет дополнительный фазовый сдвиг на 180 градусов. При значениях m=0.5-1 появляется вторая пара гармонических колебаний с боковыми частотами
С ростом m амплитуда боковых составляющих увеличивается, в то время как амплитуда несущего колебания уменьшается. Спектр сигнала с угловой модуляцией при произвольном значении индекса m. Для простейшего случая однотонального ЧМ- и ФМ-сигнала можно найти общее выражение спектра, справедливое при любом значении индекса модуляции m. Математическая модель ЧМ- или ФМ-сигнала с любым значением индекса модуляции:
Спектр однотонального сигнала с угловой модуляцией в общем случае содержит бесконечное число составляющих, частоты которых равны В теории функций Бесселя доказывается, что функции с положительными и отрицательными индексами связаны между собой соотношением:
Поэтому начальные фазы боковых колебаний с частотами
Как правило, реальные ЧМ- и ФМ-сигналы характеризуются условием
Таким образом, сигнал с угловой модуляцией занимает полосу частот, приблизительно равную удвоенной девиации частоты. Для передачи АМ-сигнала требуется полоса частот, равная
Спектральные диаграммы сигнала с угловой модуляцией при двух значениях индекса m (амплитуды представлены в относительном масштабе). Угловая модуляция при негармоническом модулирующем сигнале. Интересная особенность колебаний с угловой модуляцией проявляется в случае, когда модулирующий сигнал не является гармоническим. Рассмотрим, для простоты сигнал, промодулированный лишь двумя низкими частотами:
(5.32) Положим, что парциальные индексы модуляции Выполнив несколько громоздкие, но вполне элементарные тригонометрические преобразования, представим исходный сигнал в виде суммы:
(5.33)
Следует обратить внимание на то, что в спектре рассматриваемого сигнала, помимо частот
Спектральная диаграмма сигнала с двухтональной угловой модуляцией при малых значениях парциальных индексов модуляции Можно показать, что в общем случае, когда угловая модуляция осуществляется группой низкочастотных колебаний с частотами
(5.34) Таким образом, при прочих равных условиях спектр колебания со сложной угловой модуляцией гораздо богаче спектра аналогичного АМ-сигнала. Угловую модуляцию, в отличие от амплитудной, называют модуляцией нелинейного типа.
|

 передаваемое сообщение
передаваемое сообщение  изменяет либо частоту
изменяет либо частоту  , либо начальную фазу
, либо начальную фазу  ; амплитуда
; амплитуда  остаётся неизменной. Поскольку аргумент гармонического колебания
остаётся неизменной. Поскольку аргумент гармонического колебания 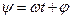 , называемый полной фазой, определяет текущее значение фазового угла, такие сигналы получили название сигналов с угловой модуляцией.
, называемый полной фазой, определяет текущее значение фазового угла, такие сигналы получили название сигналов с угловой модуляцией. связана с сигналом
связана с сигналом  (5.20)
(5.20) – значение частоты в отсутствие полезного сигнала; k - некоторый коэффициент пропорциональности. Модуляцию, отвечающую соотношению (5.20) называются фазовой модуляцией (ФМ):
– значение частоты в отсутствие полезного сигнала; k - некоторый коэффициент пропорциональности. Модуляцию, отвечающую соотношению (5.20) называются фазовой модуляцией (ФМ): (5.21)
(5.21)
 растёт во времени быстрее, чем по линейному закону. При уменьшении значений модулирующего сигнала происходит спад скорости роста
растёт во времени быстрее, чем по линейному закону. При уменьшении значений модулирующего сигнала происходит спад скорости роста  . В общем случае, когда сигнал S(t) изменяет знак, принято различать девиацию фазы вверх
. В общем случае, когда сигнал S(t) изменяет знак, принято различать девиацию фазы вверх 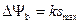 и девиацию фазы вниз
и девиацию фазы вниз  . Мгновенная частота
. Мгновенная частота  сигнала с угловой модуляцией определяется как первая производная от полной фазы по времени:
сигнала с угловой модуляцией определяется как первая производная от полной фазы по времени: (5.22)
(5.22) (5.23)
(5.23) (5.24)
(5.24)
 и девиация частоты вниз
и девиация частоты вниз  .
. ,
, - девиация частоты сигнала.
- девиация частоты сигнала. ,
, – некоторый постоянный фазовый угол.
– некоторый постоянный фазовый угол.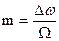 (5.25)
(5.25) , и выразим мгновенное значение ЧМ-сигнала в виде:
, и выразим мгновенное значение ЧМ-сигнала в виде: (5.26)
(5.26) , а при ЧМ
, а при ЧМ  .
. . Для этого преобразуем формулу (5.26) следующим образом:
. Для этого преобразуем формулу (5.26) следующим образом: (5.27)
(5.27)
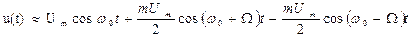 (5.28)
(5.28) . Индекс m играет здесь такую же роль как коэффициент М при АМ. Однако можно обнаружить и существенное различие спектров АМ-сигнала и колебания с угловой модуляцией.
. Индекс m играет здесь такую же роль как коэффициент М при АМ. Однако можно обнаружить и существенное различие спектров АМ-сигнала и колебания с угловой модуляцией.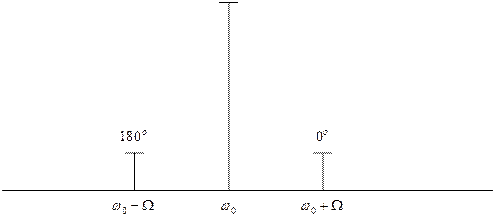
 , затем третья пара и так далее. Возникновение новых спектральных составляющих приводит к перераспределению энергии по спектру.
, затем третья пара и так далее. Возникновение новых спектральных составляющих приводит к перераспределению энергии по спектру.
 (5.29)
(5.29) (m) – функция Бесселя k- того порядка от аргумента m.
(m) – функция Бесселя k- того порядка от аргумента m. ; амплитуды этих составляющих пропорциональные значениям
; амплитуды этих составляющих пропорциональные значениям  .
.
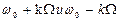 совпадают, если k- чётное число, и отличаются на 180 градусов, если k- нечётное. С ростом индекса модуляции расширяется полоса частот, занимаемая сигналом. Обычно полагают, что допустимо пренебречь всеми спектральными составляющими с номерами
совпадают, если k- чётное число, и отличаются на 180 градусов, если k- нечётное. С ростом индекса модуляции расширяется полоса частот, занимаемая сигналом. Обычно полагают, что допустимо пренебречь всеми спектральными составляющими с номерами  . Отсюда следует оценка практической ширины спектра сигнала с угловой модуляцией.
. Отсюда следует оценка практической ширины спектра сигнала с угловой модуляцией. (5.30)
(5.30) . В этом случае
. В этом случае (5.31)
(5.31) , то есть в m раз меньшая. Большая широкополосность ЧМ- и ФМ-сигналов обуславливает их гораздо более высокую помехоустойчивость по сравнению с АМ-сигналами.
, то есть в m раз меньшая. Большая широкополосность ЧМ- и ФМ-сигналов обуславливает их гораздо более высокую помехоустойчивость по сравнению с АМ-сигналами.


 малы настолько, что можно пользоваться приближёнными выражениями для косинуса и синуса:
малы настолько, что можно пользоваться приближёнными выражениями для косинуса и синуса:  .
.
 , присутствуют так называемые комбинационные частоты
, присутствуют так называемые комбинационные частоты  с четырьмя возможными знаками. Амплитуды этих составляющих зависят от произведения парциальных индексов модуляции.
с четырьмя возможными знаками. Амплитуды этих составляющих зависят от произведения парциальных индексов модуляции.
 и парциальными индексами
и парциальными индексами  соответственно, спектральное представление сигнала таково:
соответственно, спектральное представление сигнала таково:



