Моментные функции случайных процессов
Вполне удовлетворительные для практики, хотя и менее детальные, характеристики случайных процессов можно получить, вычисляя моменты тех случайных величин, которые наблюдаются в сечениях этих процессов. Поскольку в общем случае эти моменты зависят от временных аргументов, они получили название моментных функций. Для техники наибольшее значение имеют три моментные функции низших порядков, называемые математическим ожиданием, дисперсией и функцией корреляции. Математическое ожидание – начальный момент I-го порядка:
есть среднее значение процесса X(t) в текущий момент времени t: усреднение проводится по всему ансамблю реализаций процесса. Дисперсия центральный момент II-го порядка:
позволяет судить о степени разброса мгновенных значений, принимаемых отдельными реализациями в фиксированном сечении t, относительно среднего значения. Двумерный центральный момент II-го порядка.
(6.7) называется функцией корреляции случайного процесса X(t). Эта моментная функция характеризует степень статистической связи тех случайных величин, которые наблюдаются при
|
(6.5)
(6.6)
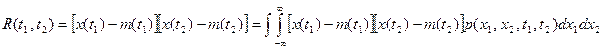
. Из сравнения формул (6.6) и (6.7) видно, что при совмещении сечений функция корреляции численно равна дисперсии:
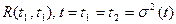(6.8)
